真空中两个完全相同、带异种电荷的导体小球A和B(视为点电荷),A带电荷量为+4Q,B带电荷量为-2Q,彼此间的引力为F.把两导体小球互相接触后再移回原来各自的位置,这时A 和B之间的作用力为F′,则F与F′之比为( )
| A.8:3 | B.8:1 | C.1:8 | D.4:1 |
带等量异种电荷的两个相同的金属小球A、B相隔L固定,两球之间的吸引力的大小是F,今让第三个不带电的相同金属小球C先后与A、B两球接触后移开.这时,A、B两球之间的库仑力的大小是( )
A.F B.F/4 C.F/8 D.3F/8
如图所示为两个固定在同一水平面上的点电荷, 距离为d, 电荷量分别为+ Q 和- Q。在它们的水平中垂线上固定一根长为L、内壁光滑的绝缘细管,有一电荷量为+q的小球以初速度v0从管口射入,则小球
| A.速度先增大后减小 |
| B.受到的库仑力先做负功后做正功 |
C.受到的库仑力最大值为 |
D.管壁对小球的弹力最大值为 |
对于库仑定律,下面说法正确的是( )
A.只要是计算真空中两个静止点电荷间的相互作用力,就可以使用公式 |
| B.两个带电小球即使相距非常近,也能用库仑定律 |
| C.相互作用的两个点电荷,带电量大的受到的力大, 带电量小的受到的力小 |
| D.当两个半径为r的带电金属球心相距为4r时,对于它们之间相互作用的静电力大小,只取决于它们各自所带的电荷量 |
在真空中有两个点电荷,相距20cm,Q1=+2×10﹣8库仑,Q2=﹣8×10﹣8库仑,则它们相互作用的静电力的大小为 N(已知静电力常量k=9.0×109N•m2/C2)
如图所示,两根细线拴着两个静止的质量相同的小球A、B。上、下两根细线中的拉力分别是TA、TB。现在使A、B带同种电荷,再次静止。上、下两根细线拉力分别为TA′、TB′,则()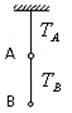
A. 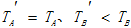
B. 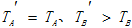
C. 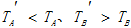
D. 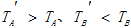
真空中有两个相同的带电金属小球A和B,相距为r,带电量分别为q和2q,它们之间相互作用力的大小为F.有一个不带电的金属球C,大小跟A.B相同,当C跟A.B小球各接触一次后拿开,再将A.B间距离变为2r,那么A.B间的作用力的大小可为( )
A.5F/64 B.0 C.3F/32 D.5F/16
如图所示,真空中有相距为L=3.0m的A、B两点放置着等量同种正点电荷Q=3.0×10-6C,现在A、B连线的中垂线上放一个不带电的导体棒,棒内有一点P(恰好落在中垂线上),且∠PAB=300,已知静电力常量k=9.0×109 N·m2/C2,当棒达到静电平衡后,求: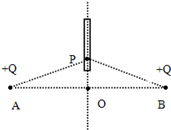
(1)两点电荷间的库仑力大小
(2)棒上感应电荷在棒内P点产生的场强E感的大小和方向
由库仑定律可知,真空中两个静止的点电荷,带电量分别q1和q2,其间距离为r时,它们之间的相互作用力的大小为F=kq1q2/r2,式中k为静电力常量。若用国际单位制的基本单位表示,k的单位应为
A.kg·A2·m2 B.kg·m3·A-2 ·s-2 C.kg·A-2·m3·s-4 D.N·m2·C-2
关于物理学家和他们的贡献,下列说法中正确的是( )
| A.奥斯特发现了电流的热效应 |
| B.库仑提出了库仑定律,密立根最早实验测得元电荷e的数值 |
| C.开普勒发现了行星运动的规律,并通过实验测出了万有引力常量 |
| D.牛顿不仅发现了万有引力定律,而且提出了场的概念 |
如图,真空中xOy平面直角坐标系上的A、B、C三点构成等边三角形,边长L=2.0 m.若将电荷量均为q=+2.0×10-6 C的两点电荷分别固定在A、B点,已知静电力常量k=9×109 N·m2/C2,求: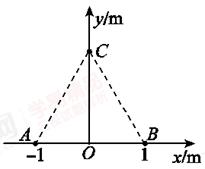
(1)两点电荷间的库仑力大小;
(2)C点的电场强度的大小和方向.
如图,同一直线上有A、B、C三点,A、B处均固定着一正电荷,C处的负电荷受A、B的库仑力的合力记为F,若将C处的电荷向B移近一些,力F会( )

A. 变小 B. 变大 C. 不变 D. 变大、变小均有可能
如图,真空中xOy平面直角坐标系上的ABC三点构成等边三角形,边长L=2.0m,若将电荷量均为q=+2.0×10﹣6C的两点电荷分别固定在A、B点,已知静电力常量k=9.0×109N•m2/C2,求:
(1)两点电荷间的库仑力大小;
(2)C点的电场强度的大小和方向.
如图所示,悬挂在O点的一根不可伸长的绝缘细线下端有一个带电量不变的小球A.在两次实验中,均缓慢移动另一带同种电荷的小球B.当B到达悬点O的正下方并与A在同一水平线上,A处于受力平衡时,悬线偏离竖直方向的角度为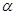 ,若两次实验中B的电量分别为
,若两次实验中B的电量分别为 和
和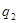 ,角度为
,角度为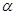 分别为
分别为 和
和 则
则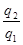 为
为

A.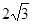 B.
B.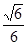 C.
C. D.
D.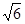
试题篮
()