高中物理库仑定律选择题

真空中有两个固定的带正电的点电荷，其电量Q₁＞Q₂，点电荷q置于Q₁、Q₂连线上某点时，正好处于平衡，则

A．q一定是正电荷	B．q一定是负电荷
C．q离Q2比离Q1远	D．q离Q2比离Q1近

在两个固定的等量同种点电荷形成的电场中， 有一电量为q的粒子，仅在电场力作用下运动，某时刻该粒子位于两点电荷连线的中垂线上M点，如下图所示，则该粒子的运动不可能是以下哪种形式

A．加速直线运动	B．变加速曲线运动
C．减速直线运动	D．匀加速曲线运动

已知真空中两个点电荷间的库仑力的大小为F，若将这两个点电荷的电荷量都增到原来的2倍，并将这两个点电荷之间的距离也增到原来的2倍，经过上述调整之后，两点电荷间的库仑力的大小为(   )

A．F

B．2F

C．4F

D．16F

如图所示，M、N为两个固定的等量同种正电荷，在其连线的中垂线上的P点放一个静止的负电荷(重力不计)，下列说法中正确的是(  )

A．从P到O，可能加速度越来越小，速度越来越大

B．从P到O，可能加速度先变大，再变小，速度越来越大

C．越过O点后，加速度一直变大，速度一直变小

D．越过O点后，加速度一直变小，速度一直变小

如图所示，M、N为两个等量同种电荷，在其连线的中垂线上的P点放一静止的点电荷q（负电荷），不计重力，下列说法中正确的是（         ）

A．点电荷在从P到O的过程中，加速度越来越大，速度也越来越大

B．点电荷在从P到O的过程中，加速度越来越小，速度越来越大

C．点电荷运动在O点时加速度为零，速度达最大值

D．点电荷越过O点后，速度越来越小，加速度越来越大，直到粒子速度为零

如图所示，一电子沿等量异种电荷的中垂线由 A→O→B匀速运动，电子重力不计，则电子除受电场力外，所受的另一个力的大小和方向变化情况是（   ）

A．先变大后变小，方向水平向左

B．先变大后变小，方向水平向右

C．先变小后变大，方向水平向左

D．先变小后变大，方向水平向右

如图所示，光滑绝缘水平桌面上有A、B两个带电小球（可以看成点电荷），A球带电量为+2q，B球带电量为-q，将它们同时由静止开始释放，A球加速度的大小为B球的3倍．现在AB中点固定一个带电小球C（也可看作点电荷），再同时由静止释放A、B两球，释放瞬间两球加速度大小相等．则C球带电量可能为 （   ）

A．q          B．q         C．q        D．q

如图，在光滑绝缘的水平桌面上方固定着电荷量大小相等的两个点电荷，一个带电小球（可视为点电荷）恰好围绕O点在桌面上做匀速圆周运动．已知O、q₁、q₂在同一竖直线上，下列判断正确的是（ ）

A．q1、q2为异种电荷

B．圆轨道上的电场强度处处相同

C．圆轨道上的电势处处相等

D．点电荷q1对小球的静电力是吸引力

如图所示，两个质量分别为m₁和m₂的小球，各用细线悬挂在同一点.两个小球分别带有电荷量为q₁和q₂的同种电荷，两悬线与竖直方向的夹角分别是α和β，两球位于同一水平线上，则下列说法中正确的是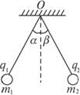

A．若m1=m2，则一定有α=β	B．若q1=q2，则一定有α=β
C．若m1＞m2，则一定有α＜β	D．若q1＞q2，则一定有α＞β

带等量异种电荷的点电荷固定在空间的A.B两点，CD为AB的中垂线，O为垂足，一个α粒子在由AB.CD确定的平面内运动．如图的四条弧形虚线中，哪些是α粒子的可能轨迹(  )

A．①③   B．②④       C．③       D．①

点电荷A和B，分别带正电和负电，电荷量分别为4Q和Q，在A、B连线上，如图所示，电场强度为零的地方在（　　)

A．A和B之间       B．A的右侧      
C．B的左侧        D．A的右侧及B的左侧

两个质量分别是m₁、m₂的小球，各用丝线悬挂在同一点，当两球分别带同种电荷，且电荷量分别为q₁、q₂时，两丝线张开一定的角度θ₁、θ₂，两球位于同一水平线上，如图所示，则下列说法正确的是(         )

A．若m1＜m2，则θ1>θ2	B．若m1＝m2，则θ1＝θ2
C．若m1>m2，则θ1>θ2	D．若q1＝q2，则θ1＝θ2

图中虚线为一组间距相等的同心圆，圆心处固定一带正电的点电荷。一带电粒子以一定初速度射入电场，实线为粒子仅在电场力作用下的运动轨迹，a、b、c三点是实线与虚线的交点。则该粒子(     )

A．该粒子带负电

B．在c点受力最大

C．在b点的电势能大于在c点的电势能

D．由a点到b点的动能变化等于由b点到c点的动能变化

两个可以自由移动的点电荷分别放在A、B两处，如图1所示，A处电荷带正电Q₁，B处电荷带负电Q₂，且Q₂ = 4Q₁，另取一个可以自由移动的点电荷Q₃，放在AB直线上，欲使整个系统处于平衡状态，则（  ）

A．Q₃为正电荷，且放于A左方
B．Q₃为负电荷，且放于B右方
C．Q₃为负电荷，且放于AB之间
D．Q₃为正电荷，且放于B右方

如图示，相互垂直的固定绝缘光滑挡板PO、QO，竖直放置在重力场中，a、b为两个带有同种电量的小球（可以近似看成点电荷），当用水平向左作用力F作用于b时，a、b紧靠挡板处于静止状态．现若稍改变F的大小，使b稍有向左移动一段小距离，则当a、b重新处于静止状态后（ ）

A．ab间的电场力增大	B．作用力F将减小
C．系统重力势能增加	D．系统的电势能将增加