高中物理匀强电场选择题

如图，a、b、c、d是匀强电场中的四个点，它们正好是一个梯形的四个顶点．电场线与梯形所在的平面平行．ab平行cd，且ab边长为cd边长的一半，已知a点的电势是3 V，b点的电势是5 V，c点的电势是7 V．由此可知，d点的电势为（　　）

A．1 V

B．2 V

C．3 V

D．4 V

下列关于U＝Ed说法正确的是 (　　)

A．在电场中，E跟U成正比，跟d成反比

B．对于任何电场，U＝Ed都适用

C．U＝Ed只适用于匀强电场，d是电场中任意两点间距离

D．U＝Ed只适用于匀强电场，d是沿着电场线方向两点间距离

如图所示，圆O所在的平面内有匀强电场存在，电场方向与圆面平行。一个带正电荷的微粒（不计重力）从图中A点出发，以相同的初动能在圆内向各个方向运动，已知图中AB是圆的一条直径，∠BAC=30°，已知只有当该微粒从图中C点处离开圆面时的动能才能达到最大值，则平面内的电场线方向为（     ）

A．沿A→B方向	B．沿A→C方向
C．沿O→C方向	D．沿B→C方向

如图1所示，匀强电场场强为E，A与B两点间的距离为d，AB与电场线夹角为,则A与B两点间的电势差为(      )

A．Ed

B．Edcos

C．Edsin

D．Edtan

空间有一沿x轴对称分布的电场，其电场强度E随X变化的图像如图所示。下列说法正确的是（   ）

A．O点的电势最低

B．X2点的电势最高

C．X1和- X1两点的电势相等

D．X1和X3两点的电势相等

关于重力势能和电势能，下列说法中正确的是

A．两种势能都是物体单独具有的

B．两种势能的值都与零势能位置选择无关

C．两种势能的变化量，都可以用力做的功来衡量

D．两种势能的值都可正可负，所以都是矢量

对公式E=U_ab/d的理解，下列说法正确的是（    ）

A．此公式适用于计算任何电场中a、b两点间的电势差

B．a点和b点间距离越大，则这两点的电势差越大

C．匀强电场中a、b两点沿电场线的距离越大，则电场强度越小

D．公式中的d是匀强电场中a、b所在的两等势面之间的距离

如图所示，在一个匀强电场(图中未画出)中有一个四边形ABCD，其中，M为AD的中点，N为BC的中点．一个带正电的粒子从A点移动到B点，电场力做功为W_AB=2.0×10^-9J；将该粒子从D点移动到C点，电场力做功为W_DC=4.0×l0^-9J．则以下分析正确的是：

A．若将该粒子从M点移动到N点，电场力做功为W_MN=3.0×10^-9J
B．若将该粒子从M点移动到N点，电场力做功W_MN有可能大于4.0×l0^-9J
C．若A、B之间的距离为1cm，粒子的电量为2×10^-7C，该电场的场强一定是E=1V/m
D．若粒子的电量为2×10^-9C，则A、B之间的电势差为1V

如图（a）所示，在x轴上的两点分别放有-Ｑ和+4Ｑ两个点电荷，位置坐标分别为0和1。图（b）是反映沿x轴电势分布情况的图线，正确是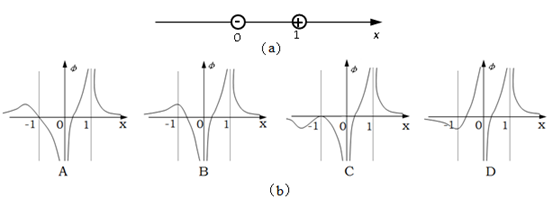

边长为L的正立方体区域内存在着匀强电场，电场强度为E，a、b为正方体的两个顶点，则a、b两点的电势差U_ab不可能的是

A．Uab = -1.5EL	B．Uab = 0
C．Uab = 2EL	D．Uab = EL

在点电荷 Q形成的电场中有一点A，当一个－q的检验电荷从电场的无限远处被移到电场中的A点时，电场力做的功为W，则检验电荷在A点的电势能及电场中A点的电势分别为：（     ）

有一电场的电场线如图所示，场中A、B两点电场强度的大小和电势分别为、和、表示，则（  ）

A、> >      B、> <     
C、< >       D、<  <

对于点电荷的电场,我们取无限远处作零电势点,无限远处电场强度也为零,那么以下说法正确的是(     )

A．电势为零的点，电场强度一定为零，反之亦然

B．电势为零的点，电场强度不一定为零，但电场强度为零的点，电势一定为零

C．电场强度为零的点，电势不一定为零；电势为零的点，场强不一定为零

D．场强为零的点，电势不一定为零，电势为零的一点，电场强度一定为零

如图所示，A、B、C、D、E、F为匀强电场中一个正六边形的六个顶点，A、B、C三点的电势分别为1V、2V、5V。则下列说法中正确的是    (    )

A．D、E、F三点的电势分别为7V、6V、3V
B．电荷量为1.6X10^一19C的正点电荷在D点的电势能为1.12X10^-18J
C．将电荷量为1.6X10^-19C的正点电荷从E点移到F点，电场力做的功为3.2X10^-19J
D．将电荷量为1.6X10^{一 19C}的负点电荷从F点移到A点，
电荷的电势能减少了3.2X10^-19J

如图所示，A、B、C、D是匀强电场中一正方形的四个顶点，已知A、B、C三点的电势分别为Φ_A＝15 V，Φ_B＝3V，Φ_C＝－3V，由此可得D点电势Φ_C是（ ）。

A.3V     B.6V     C.9V     D.-9V