高中物理电磁场选择题

利用霍尔效应制作的霍尔元件，广泛应用于测量和自动控制等领域。如图是霍尔元件的工作原理示意图,磁感应强度B垂直于霍尔元件的工作面向下，通入图示方向的电流I， C、D两侧面会形成电势差U_CD，下列说法中正确的是

A．电势差U_CD仅与材料有关
B．若霍尔元件的载流子是自由电子，则电势差U_CD＜0
C．仅增大C、D间的宽度时,电势差U_CD变大
D．在测定地球两极上方的地磁场强弱时,元件的工作面应保持水平

如图所示，MN是纸面内的一条直线，其所在空间充满与纸面平行的匀强电场或与纸面垂直的匀强磁场(场区都足够大)，现有一个重力不计的带电粒子从MN上的O点以水平初速度v₀射入场区，下列判断正确的是： 
 

A．如果粒子回到MN上时速度增大，则该空间存在的场一定是电场。

B．如果粒子回到MN上时速度大小不变，则该空间存在的场可能是电场。

C．若只改变粒子的初速度大小，发现粒子再回到MN上时与其所成的锐角夹角不变，则该空间存在的场一定是磁场。

D．若只改变粒子的初速度大小，发现粒子再回到MN上所用的时间不变，则该空间存在的场一定是磁场。

如图所示，一形状为抛物线的光滑曲面轨道置于竖直平面内，轨道的下半部处在一个水平向外的磁场中，磁场的上边界是的直线(图中虚线所示)，一个小金属环从抛物线上处以速度沿抛物线下滑。假设抛物线足够长，且不计空气阻力，则金属环沿抛物线运动的整个过程中损失的机械能的总量为

A．若磁场为匀强磁场，

B．若磁场为匀强磁场，

C．若磁场为非匀强磁场，

D．若磁场为非匀强磁场，

如图，一个质量为m、带电量为+q的圆环，可在水平放置的足够长的粗糙细杆上滑动，细杆处于磁感应强度为B的匀强磁场中。现给圆环一个水平向右的初速度v₀，在以后的运动中下列说法正确的是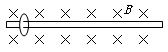
                           （   ）

A．圆环可能做匀减速运动

B．圆环不可能做匀速直线运动

C．圆环克服摩擦力所做的功一定为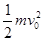

D．圆环克服摩擦力所做的功可能为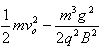

如图所示，质量为m，带电荷量为＋q的P环套在固定的水平长直绝缘杆上，整个装置处在垂直于杆的水平匀强磁场中，磁感应强度大小为B.现给环一向右的初速度v₀，则                                                        (　　)

A．环将向右减速，最后匀速
B．环将向右减速，最后停止运动
C．从环开始运动到最后达到稳定状态，损失的机械能是mv
D．从环开始运动到最后达到稳定状态，损失的机械能是mv－m²

如图所示，一质量为m、电荷量为+q的带电粒子，（不计粒子重力），在O点以某一初速度与水平成60⁰射入磁场区域Ⅰ，粒子沿曲线Oabc运动，Oa、ab、bc都是半径相同的圆弧。粒子在每段圆弧上运动的时间都为t。现规定垂直纸面向外为磁感应强度的正方向，则水平宽度相同的磁场区域Ⅰ、Ⅱ、Ⅲ三部分的磁感应强度B随x变化的关系是下图中的：

有关洛伦兹力和安培力的描述，正确的是（）

A．	通电直导线在匀强磁场中一定受到安培力的作用
B．	安培力是大量运动电荷所受洛伦兹力的宏观表现
C．	带电粒子在匀强磁场中运动受到的洛伦兹力做正功
D．	通电直导线在磁场中受到的安培力方向与磁场方向平行

如图，在x>0、y>0的空间中有恒定的匀强磁场，磁感应强度的方向垂直于oxy平面向里，大小为B。现有一质量为m电量为q的带电粒子，在x轴上到原点的距离为x₀的P点，以平行于y轴的初速度射入此磁场， 在磁场作用下沿垂直于y轴的方向射出此磁场。不计重力的影响。由这些条件可知

A．能确定粒子通过y轴时的位置

B．能确定粒子速度的大小

C．能确定粒子在磁场中运动所经历的时间

D．以上三个判断都不对

一根长0.20m、通有2.0A电流的通电直导线，放在磁感应强度为0.50T的匀强磁场中，受到的安培力大小不可能是（    ）

A．0N

B．0.10N

C．0.20N

D．0.40N

如图6-7所示，矩形线圈abcd放置在水平面内，磁场方向与水平面成α角，已知sinα＝，线圈面积为S，匀强磁场的磁感应强度为B，则通过线圈的磁通量为（　　）

图6-7

A．BS

B．

C．

D．

按照麦克斯韦的电磁理论,下列说法中正确的是(    )

A．变化的磁场周围产生变化的电场

B．均匀变化的磁场周围产生均匀变化的电场

C．恒定电流周围产生稳定的磁场

D．在电场的周围一定产生磁场,在磁场的周围一定产生电场

如图所示，在一个半径为R的圆形区域内存在着匀强磁场，磁场方向垂直于圆面向里.一个带电粒子从磁场边界的A点以指向圆心O的方向进入磁场区域内，粒子将做圆周运动到达磁场边界的C点，但在粒子经过D点时，恰好与一个原来静止在该点的不带电的粒子碰撞后结合在一起形成新粒子，关于这个新粒子的运动情况，下列判断正确的是（   ）

A．新粒子的运动半径将减小，可能到达F点

B．新粒子的运动半径将增大，可能到达E点

C．新粒子的运动半径将不变，仍然到达C点

D．新粒子在磁场中的运动时间将变长