中国渔政船主要用于渔场巡视并监督、检查渔船执行国家渔业法规的情况,保护水域环境,同时有到有争议的海域巡逻宜示主权的作用.一艘质量为m="500" t的渔政船,从某码头由静止出发做直线运动去执行任务,先保持发动机的输出功率等于倾定功率不变,经一段时间后,达到最大行驶速度vm="20" m/s。此时,渔政船的船长突然发现航线正前方s="480" m处有一艘我国的拖网渔船以v="6" m/s的速度沿垂直航线方向匀速运动,且此时渔船船头恰好位于渔政船的航线上,渔政船船长立即下令采取制动措施,附加了恒定的制动力F=1.5 105N,结果渔船的拖网越过渔政船的航线时,渔政船也恰好从该点通过,从而避免了事故的发生.已知渔船连同拖网总长度L="240" m(不考虑拖网渔船的宽度和渔政船的长度),假定水对渔政船阻力的大小恒定不变,求:
105N,结果渔船的拖网越过渔政船的航线时,渔政船也恰好从该点通过,从而避免了事故的发生.已知渔船连同拖网总长度L="240" m(不考虑拖网渔船的宽度和渔政船的长度),假定水对渔政船阻力的大小恒定不变,求:
(1)渔政船减速时的加速度a;
(2)渔政船的颇定功率P.
甲车以10m/s的速度在平直的公路上匀速行驶,乙车以4m/s的速度与甲车平行同向做匀速直线运动,甲车经过乙车旁边开始以1m/s2的加速度刹车,从甲车刹车开始计时,
求:(1)乙车在追上甲车前,两车相距的最大距离;
(2)乙车追上甲车所用的时间。
为了安全,在公路上行驶的汽车之间应保持必要的安全距离。广深高速公路的最高限速为v0=144km/h,若前方车辆突然停止,后方车辆司机从发现这一情况,经操纵刹车,到汽车开始减速所经历的时间t=0.5s(即反应时间),若刹车时汽车的加速度大小为4m/s2。求:此高速公路上汽车间的距离s至少应为多少?
(19分) 如图所示,水平面上紧靠放置着等厚的长木板B、C(未粘连),它们的质量均为M=2kg。在B木板的左端放置着质量为m=1kg的木块A(可视为质点)。A与B、C间的动摩擦因数均为μ1=0.4,B、C与水平面间的动摩擦因数均为μ2=0.1,滑动摩擦力等于最大静摩擦力。开始整个系统处于静止,现对A施加水平向右的恒定拉力F=6N,测得A在B、C上各滑行了1s后,从C的右端离开木板。
求:⑴木板B、C的长度LB、LC;
⑵若在木块A滑上C板的瞬间撤去拉力F,木块A从开始运动到再次静止经历的总时间t(此问答案保留3位有效数字)。
如图甲所示,在y=0和y=2m之间有沿着x轴方向的匀强电场,MN为电场区域的上边界,在x轴方向范围足够大。电场强度随时间的变化如图乙所示,取x轴正方向为电场正方向。现有一个带负电的粒子,粒子的比荷为 =1.0×10-2C/kg,在t=0时刻以速度v0=5×102 m/s从O点沿y轴正方向进入电场区域,不计粒子重力。求:
=1.0×10-2C/kg,在t=0时刻以速度v0=5×102 m/s从O点沿y轴正方向进入电场区域,不计粒子重力。求:
(1)粒子通过电场区域的时间;
(2)粒子离开电场时的位置坐标;
(3)粒子通过电场区域后沿x方向的速度大小。
质量为m=1.0 kg的小滑块(可视为质点)放在质量为M=3.0 kg的长木板的右端,木板上表面光滑,木板与地面之间的动摩擦因数为μ=0.2,木板长L=1.0 m.开始时两者都处于静止状态,现对木板施加水平向右的恒力F=12 N,如图所示,经一段时间后撤去F。为使小滑块不掉下木板,试求:用水平恒力F作用的最长时间(g取10 m/s2)。
如图甲所示,某同学用轻绳通过定滑轮提升一重物,运用传感器(未在图中画出)测得此过程中不同时刻被提升重物的速度v与对轻绳的拉力F,并描绘出v- 图象.假设某次实验从静止开始提升重物,所得的图象如图乙所示,其中线段AB与纵轴平行,它反映了被提升重物在第一个时间段内v和
图象.假设某次实验从静止开始提升重物,所得的图象如图乙所示,其中线段AB与纵轴平行,它反映了被提升重物在第一个时间段内v和 的关系;线段BC的延长线过原点,它反映了被提升重物在第二个时间段内v和
的关系;线段BC的延长线过原点,它反映了被提升重物在第二个时间段内v和 的关系;第三个时间段内拉力F和速度v均为C点所对应的大小保持不变,因此图象上没有反映.实验中还测得重物由静止开始经过t=1.4 s,速度增加到vC=3.0 m/s,此后物体做匀速运动.取重力加速度g=10 m/s2,绳重及一切摩擦力和阻力均忽略不计.
的关系;第三个时间段内拉力F和速度v均为C点所对应的大小保持不变,因此图象上没有反映.实验中还测得重物由静止开始经过t=1.4 s,速度增加到vC=3.0 m/s,此后物体做匀速运动.取重力加速度g=10 m/s2,绳重及一切摩擦力和阻力均忽略不计.
(1)求第一个时间段内重物的加速度有多大?
(2)求第二个时间段内牵引力的功率有多大?
(3)求被提升重物在第二个时间段内通过的路程.
如图所示,半径R=1m的光滑绝缘的1/4圆弧与水平绝缘的传送带相切且相接与B点,传送带的顺时针运行,速度恒为v0=1m/s,长L=2.875m。在整个空间中加上水平向左的匀强电强E= 2×104V/m,现将质量m=1kg,电量q=+1.0×10-4C的滑块从A点(A点与圆心O点等高)无初速度释放。已知滑块与传送带间的动摩擦因数为μ=0.1,g=10m/s2,试求:
(1)滑块滑到B点时的速度大小?
(2)滑块在传送带上运动时间?
(3)滑块在传送带上运动摩擦生的热Q?
一平板车,质量M =100kg,停在水平路面上,车身的平板离地面的高度h =1.25m。一质量m =50kg的滑块置于车的平板上,它到车板末端的距离b=1.00m,与车板间的动摩擦因数μ=0.20,如图所示,今对平板车施一水平方向的恒力,使车向前行驶,结果滑块从车板上滑落,滑块刚离开车板的时刻,车向前行驶的距离s0=2.00m。求滑块落地时,落地点到车尾的距离s(不计路面与平板车间以及轮轴的摩擦,g=10m/s2)
传送皮带在生产生活中有着广泛的应用,一运煤传送皮带与水平面夹角为30°,以2m/s的恒定速度顺时针运行。现将一质量为10kg的煤块(视为质点)轻放于底端,经一段时间送到高2m的平台上,煤块与皮带间的动摩擦因数为μ=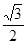 ,取g=10m/s2,求
,取g=10m/s2,求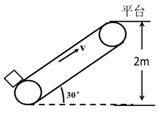
(1)煤块从底端到平台的时间;
(2)带动皮带的电动机由于传送煤块多消耗的电能。
在竖直平面内建立xoy直角坐标系,oy表示竖直向上方向.如图所示.已知该平面内存在沿x轴正向的区域足够大的匀强电场.一带电小球从坐标原点o沿ox方向以4J的初动能竖直向上抛出.不计空气阻力,它到达的最高位置如图中M点所示,求: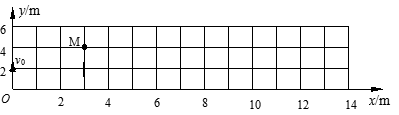
(1)小球在M点时的动能EkM.
(2)设小球落回跟抛出点在同一水平面时的位置为N,求小球到达N点时的动能EkN.
某电视台“快乐向前冲”节目中的场地设施如题图所示,AB为水平直轨道,上面安装有电动悬挂器,可以载人运动,水面上漂浮着一个半径为R,角速度为ω,铺有海绵垫的转盘,转盘的轴心离平台的水平距离为L,平台边缘与转盘平面的高度差为H.选手抓住悬挂器,可以在电动机带动下,从A点下方的平台边缘处沿水平方向做初速度为零,加速度为a的匀加速直线运动.选手必须作好判断,在合适的位置释放,才能顺利落在转盘上.设人的质量为m(不计身高大小),人与转盘间的最大静摩擦力为μmg,重力加速度为g。
① 假设选手落到转盘上瞬间相对转盘速度立即变为零,为保证他落在距圆心 以内不会被甩出转盘,转盘的角速度ω应限制在什么范围?
以内不会被甩出转盘,转盘的角速度ω应限制在什么范围?
② 若已知H =" 5" m,L =" 8" m,a =" 2" m/s2,g =" 10" m/s2,且选手从某处C点释放能恰好落到转盘的圆心上,则他是从平台出发后经过多长时间释放悬挂器的?
③ 若电动悬挂器开动后,针对不同选手的动力与该选手重力关系皆为F = 0.6mg,悬挂器在轨道上运动时存在恒定的摩擦阻力,选手在运动到上面(2)中所述位置C点时,因恐惧没有释放悬挂器,但立即关闭了它的电动机,则按照(2)中数据计算悬挂器载着选手还能继续向右滑行多远的距离?
如图所示,质量M=8.0kg、长L=2.0m的薄木板静置在水平地面上,质量m=0.50kg的小滑块(可视为质点)以速度v0=3.0m/s从木板的左端冲上木板。已知滑块与木板间的动摩擦因数μ=0.20,重力加速度g取10m/s2。
(1)若木板固定,滑块将从木板的右端滑出,求:
a.滑块在木板上滑行的时间t;
b.滑块从木板右端滑出时的速度v。
(2)若水平地面光滑,且木板不固定。在小滑块冲上木板的同时,对木板施加一个水平向右的恒力F,如果要使滑块不从木板上掉下,力F应满足什么条件?(假定滑块与木板之间最大静摩擦力与滑动摩擦力相等)
如图所示,是一传送装置,其中AB段粗糙,AB段长为L=1 m,动摩擦因数μ=0.5;BC、DEN段均可视为光滑,DEN是半径为r=0.5 m的半圆形轨道,其直径DN沿竖直方向,C位于DN竖直线上,CD间的距离恰能让小球自由通过。其中N点又与足够长的水平传送带的右端平滑对接,传送带以6m/s的速率沿顺时针方向匀速转动,小球与传送带之间的动摩擦因数也为0.5。左端竖直墙上固定有一轻质弹簧,现用一可视为质点的小球压缩弹簧至A点后由静止释放(小球和弹簧不粘连),小球刚好能沿圆弧DEN轨道滑下,而始终不脱离轨道。已知小球质量m=0.2 kg ,g 取10m/s2。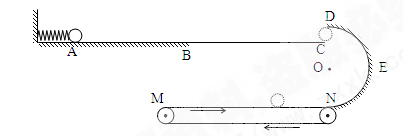
(1) 求小球到达D点时速度的大小及弹簧压缩至A点时所具有的弹性势能;
(2) 小球第一次滑上传送带后的减速过程中,在传送带上留下多长的痕迹?
(3) 如果希望小球能沿着半圆形轨道上下不断地来回运动,且始终不脱离轨道,则传送带的速度应满足什么要求?
试题篮
()