高中物理放射性同位素的应用试题

如图，在倾角为θ=37°的足够长的固定斜面底端，一小物块以某一初速度沿斜面上滑，一段时间后返回到出发点。若物块上滑所用时间t₁和下滑所用时间t₂的大小关系满足t₁∶t₂=1∶，取g＝10 m/s²，sin 37°＝0.6，cos 37°＝0.8，试求：

（1）上滑加速度a₁与下滑加速度a₂的大小之比；
（2）物块和斜面之间的动摩擦因数；
（3）若斜面倾角变为60°，并改变斜面粗糙程度，小物块上滑的同时用水平向右的推力F作用在物块上，发现物块匀减速上滑过程中加速度与推力大小无关，求此时加速度大小。

如图1所示，质量M="1" kg的木板静止在粗糙的水平地面上，木板与地面间的动摩擦因数μ₁=0.1，在木板的左端放置一个质量m="1" kg、大小可以忽略的铁块，铁块与木板间的动摩擦因数μ₂=0.4，取g="10" m/s²。

试求：（1）若木板长L="1" m，在铁块上加一个水平向右的恒力F="8" N，经过多长时间铁块运动到木板的右端？
（2）若在铁块上施加一个大小从零开始连续增加的水平向右的力F，通过分析和计算后，请在图2中画出铁块受到木板的摩擦力f₂随拉力F大小变化的图像。（设木板足够长）

如图所示，空间存在着与圆台母线垂直向外的磁场，各处的磁感应强度大小均为B，圆台母线与竖直方向的夹角为θ。一个质量为m、半径为r的通电匀质金属环位于圆台底部，0~t时间内环中电流大小恒定为I，由静止向上运动经过时间t后撤去该恒定电流并保持圆环闭合，圆环上升的最大高度为H。已知重力加速度为g，磁场的范围足够大。在圆环向上运动的过程中，下列说法正确的是

A．圆环先做加速运动后做减速运动

B．在时间t内安培力对圆环做功为mgH

C．圆环先有扩张后有收缩的趋势

D．圆环运动的最大速度为

如图甲所示，质量为M＝3.0kg的平板小车C静止在光滑的水平面上，在t＝0时，两个质量均为1.0kg的小物体A和B同时从左右两端水平冲上小车，1.0s内它们的v－t图象如图乙所示，（ g取10m/s²）求：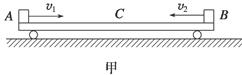
         
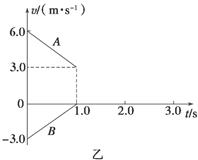
(1)小物体A和B与平板小车之间的动摩擦因数μ_A、μ_B
(2)判断小车在0～1.0s内所做的运动，并说明理由？
(3)要使A、B在整个运动过程中不会相碰，车的长度至少为多少？

如图所示，半径R＝0.4m的四分之一粗糙圆轨道MN竖直固定放置，末端N与一长L＝0.8m的水平传送带相切，水平衔接部分摩擦不计，传动轮(轮半径很小)做顺时针转动，带动传送带以恒定的速度v₀运动。传送带离地面的高度h＝1.25m，其右侧地面上有一直径D＝0.5m的圆形洞，洞口最左端的A点离传送带右端的水平距离x＝1m，B点在洞口的最右端，现使质量为m＝0.5kg的小物块从M点由静止开始释放，滑到N点时速度为2m/s，经过传送带后做平抛运动，最终落入洞中，传送带与小物块之间的动摩擦因数μ＝0.5，g取10m/s²，求：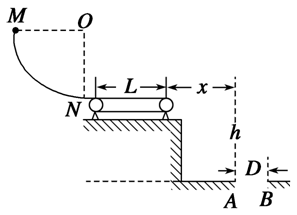

(1)小物块到达圆轨道末端N时对轨道的压力；
(2)若v₀＝3 m/s，求小物块在传送带上运动的时间；
(3)若要使小物块能落入洞中，求v₀应满足的条件。

（原创）小物块以一定的初速度自光滑斜面的底端a点上滑，最远可达b点，e为ab的中点，如图所示，已知物体由a到b的总时间为t₀，则它从e到b所用的时间为

A．

B．

C．

D．

(10分)如图，长为L=2m、质量m_A＝4kg的木板A放在光滑水平面上，质量m_B＝1kg的小物块（可视为质点）位于A的中点，水平力F作用于A.AB间的动摩擦因素μ=0.2(AB间最大静摩擦力等于滑动摩擦力，g=10m/s²)。求：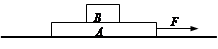
 
(1)为使AB保持相对静止，F不能超过多大？
(2)若拉力F＝12N，物块B从A板左端滑落时木板A的速度为多大？

(9分)一物体受到竖直向上拉力F的作用由静止开始向上运动，如图所示，当拉力F＝42N时，物体向上的加速度a＝4.0m/s²，不计空气阻力，g取10m/s²。求：

(1)前2s内的位移x的大小； (2)第2s末的速度v的大小； (3)物体的质量m。

汽车由静止开始匀加速前进，经过10s速度达到5m/s，则在这10s内汽车的

A．平均速度是0.5m/s	B．平均速度是2m/s
C．加速度是5m/s^2	D．位移是25m

如图所示，为车站使用的水平传送带装置模型，绷紧的传送带水平部分AB的长度L＝5m，并以v＝2m/s的速度向右运动。现将一个可视为质点的旅行包轻轻地无初速地放在传送带的A端，已知旅行包与皮带之间的动摩擦因数μ＝0.2，g＝10m/s²。求：

（1）旅行包在传送带上从A端运动到B端所用的时间t；
（2）旅行包在传送带上相对滑动时留下的痕迹的长度s。

如图所示，一质量为m=100kg的箱子静止在水平面上，与水平面间的动摩擦因素为μ=0.5。现对箱子施加一个与水平方向成θ=37°角的拉力，经t₁=10s后撤去拉力，又经t₂=1s箱子停下来。sin37°=0.6，cos37°=0.8，g＝10m/s²。求：

（1）拉力F大小；（2）箱子在水平面上滑行的位移x。

某人在零时刻开始观察一个正在做匀加速直线运动的物体，现在测出了第3s内及第7s内的位移，根据上述已知条件

A．能够求出任意一段时间内的位移

B．不能求出任意一段时间内的位移

C．不能求出任一时刻的瞬时速度

D．能够求出任一时刻的瞬时速度

如图所示，在一水平向左的匀强电场中，光滑绝缘直角三角形斜劈ABC被固定在水平面上，其斜面长L＝1.5m，倾角为θ＝37°。有一个电荷量为q＝3×10^-5C、质量为m＝4×10^-3kg的带电小物块（可视为质点）恰能静止在斜面的顶端A处。g＝10m/s²，sin37°＝0.6，cos37°＝0.8．求：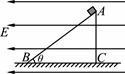

（1）AB两点间的电势差U_AB；
（2）若电场强度减小为原来的一半时小物块从A下滑到B的时间t。

一辆公共汽车进站后开始刹车，做匀减速直线运动。开始刹车后的第1s内和第2s内的位移大小依次为11m和9m。则刹车后7s内的位移是

A．24m

B．35m

C．36m

D．49m

如图甲所示，火箭发射时，速度能在10s内由0增加到100m/s；如图乙所示，汽车以8m/s的速度行驶，急刹车时能在2.5s内停下来，下列说法中正确的是

A．10s内火箭的速度改变量为100m/s^2

B．2.5s内汽车的速度改变量为8m/s

C．火箭的加速度比汽车的加速度大

D．火箭的加速度比汽车的加速度小