高中物理链式反应及其发生条件试题

如图，小球从高处下落到竖直放置的轻弹簧上，从接触弹簧开始计时到弹簧压缩到最短的过程中，下列叙述正确的是

A．小球的速度一直减少

B．小球的加速度先减小后增大

C．小球加速度的最大值，小于重力加速度

D．小球机械能守恒

如图所示，固定的竖直光滑长杆上套有质量为 $m$ 的小圆环，圆环与水平状态的轻质弹簧一端连接，弹簧的另一端连接在墙上，并且处于原长状态，现让圆环由静止开始下滑，已知弹簧原长为 $L$ ，圆环下滑到最大距离时弹簧的长度变为2 $L$ （未超过弹性限度），则在圆环下滑到最大距离的过程中（）

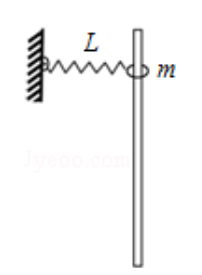
A．	圆环的机械能守恒
B．	弹簧弹性势能变化了   $\sqrt{3}mgL$
C．	圆环下滑到最大距离时，所受合力为零
D．	圆环重力势能与弹簧弹性势能之和保持不变

2012年6月24日，中国第一台自行设计、自主集成研制的深海载人潜水器——“蛟龙”号在西太平洋的马里亚纳海沟下潜深度超过7000米，预示着中国已经有能力征服全球99.8％的海底世界。假设在某次实验时，“蛟龙”号从水面开始下潜到最后返回水面共历时10min，其速度随时间的变化如图所示，则“蛟龙”号：

A．下潜的最大深度为360m

B．整个过程中的最大加速度为0.025m/s^2

C．在3～4min和6～8min内出现超重现象

D．在8～10min内机械能守恒

从地面竖直上抛一物体A的同时，在离地面高H处有相同质量的另一物体B开始做自由落体运动，两物体在空中同时到达距地面高h时速率都为v（两物体不会相碰），则下列说法正确的是(    )
A．H =" 2" h
B．物体A竖直上抛的初速度大小是物体B落地时速度大小的2倍
C．物体A、B在空中运动的时间相等
D．两物体落地前各自的机械能都守恒且两者机械能相等

如图所示，一个质量为m的物体（可视为质点）以某一初速度从A点冲上倾角为30°的固定斜面，其运动的加速度为3g/4，物体在斜面上上升的最大高度为h，则在整个过程中物体的（　 　）

A．机械能守恒

B．动能减少了3mgh/2

C．机械能减少了mgh

D．重力势能增加了3mgh/4

如图所示，下列说法正确的是（均不计摩擦、空气阻力以及滑轮质量）（ ）
A．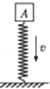
如图中，物体A以一定的初速度将弹簧压缩的过程中，物体A机械能守恒
B．
如图中，A置于光滑水平面，物体B沿光滑斜面下滑，物体B机械能守恒
C．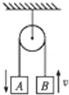
如图中，A加速下落，B加速上升过程中，A、B系统机械能守恒
D．
如图中，小球沿水平面做匀速圆锥摆运动时，小球的机械能不变

我国的月球探测计划“嫦娥工程”分为“绕、落、回”三步。“嫦娥三号”的任务是“落”。  2013年12月2日，“嫦娥三号”发射，经过中途轨道修正和近月制动之后，“嫦娥三号”探测器进入绕月的圆形轨道I。12月12日卫星成功变轨，进入远月点P、近月点Q的椭圆形轨道II。如图所示。 2013年12月14日，“嫦娥三号”探测器在Q点附近制动，由大功率发动机减速，以抛物线路径下降到距月面100米高处进行30s悬停避障，之后再缓慢竖直下降到距月面高度仅为数米处，为避免激起更多月尘，关闭发动机，做自由落体运动，落到月球表面。
已知引力常量为G，月球的质量为M，月球的半径为R，“嫦娥三号”在轨道I上运动时的质量为m， P、Q点距月球表面的高度分别为h₁、h₂。

（1）求“嫦娥三号”在圆形轨道I上运动的速度大小；
（2）已知“嫦娥三号”与月心的距离为r时，引力势能为（取无穷远处引力势能为零），其中m为此时“嫦娥三号”的质量。若“嫦娥三号”在轨道II上运动的过程中，动能和引力势能相互转化，它们的总量保持不变。已知“嫦娥三号”经过Q点的速度大小为v，请根据能量守恒定律求它经过P点时的速度大小；

如图所示，一辆汽车从凸桥上的A点匀速运动到等高的B点，以下说法中正确的是

A．由于车速不变，所以汽车从A到B过程中机械能不变

B．牵引力对汽车做的功等于汽车克服阻力做的功

C．汽车在运动过程中所受合外力为零

D．汽车所受的合外力做功为零

一个半径为r的光滑圆形槽装在小车上，小车停放在光滑的水平面上，如图所示，处在最低点的小球受击后获得水平向左的速度v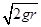＝，开始在槽内运动，则下面判断正确的是   .

A．小球和小车总动量不守恒,但水平方向的动量守恒.

B．小球和小车总机械能守恒

C．小球沿槽上升的最大高度为r

D．小球升到最高点时速度为零

如图所示，质量为M^“的光滑斜面倾角为30⁰，质量分别为M、m的两个物体通过细绳及轻弹簧连接于光滑轻滑轮两侧，斜面底端有一与斜面垂直的挡板．开始时用手按住物体M，此时M距离挡板的距离为s，滑轮两边的细绳恰好伸直，且弹簧处于原长状态．已知M=2m，空气阻力不计．松开手后，斜面体始终保持静止，则在M下滑过程中下列说法中正确的是（  ）

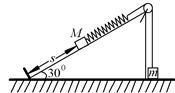
A．M和m组成的系统机械能守恒

B．当M的速度最大时（未碰到板），m与地面间的作用力不为零

C．当M的速度最大时（未碰到板），水平面对斜面的支持力为（M^’’+M+m）g

D．当m离开地面后M做匀速运动

如图所示，固定在水平面上的光滑斜面倾角为30⁰，质量分别为M、m的两个物体通过细绳及轻弹簧连接于光滑轻滑轮两侧，斜面底端有一与斜面垂直的挡板．开始时用手按住物体M，此时M距离挡板的距离为s，滑轮两边的细绳恰好伸直，且弹簧处于原长状态．已知M = 2m，空气阻力不计．松开手后，关于二者的运动下列说法中正确的是（    ）

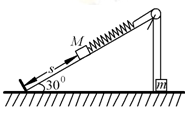
A．M和m组成的系统机械能守恒

B．当M的速度最大时，m与地面间的作用力为零

C．若M恰好能到达挡板处，则此时m的速度为零

D．若M恰好能到达挡板处，则此过程中重力对M做的功等于弹簧弹性势能的增加量与物体m的机械能增加量之和

为了验证机械能守恒定律，某同学在墙壁上固定了竖直的标尺，让小钢球在标尺附近无初速释放，然后启动数码相机的连拍功能，连拍两张照片的时间间隔为T，得到了如右图所示的照片。测量出A、B、C、D、E相邻两点间的距离依次为L₁、L₂、L₃、L₄，当地重力加速度为g。

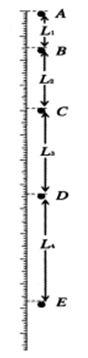
（1）为了获得钢球在C位置的动能，需要求得经C位置时的速度v_c，则v_c=___   __。
（2）钢球经E位置时的速度表示为_______。（填序号）
A．v_E=4gT    B．v_E=    C．v_E=
（3）用B、E两点验证钢球的机械能是否相等，实际得到的关系式为
_______mg（L₂+L₃+L₄）（填“>”、“<”或“=”），
原因是_______________________________________________________________。

某同学利用图示装置来研究机械能守恒问题，
设计了如下实验。A、B是质量均为m的小物块，C是质量为M的重物，A、B间由轻弹簧相连，A、C间由轻绳相连。在物块B下放置一压力传感器，重物C下放置一速度传感器，压力传感器与速度传感器相连。当压力传感器示数为零时，就触发速度传感器测定此时重物C的速度。整个实验中弹簧均处于弹性限度内，重力加速度为g。实验操作如下：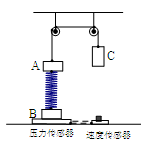

（1）开始时，系统在外力作用下保持静止，细绳拉直但张力为零。现释放C，使其向下运动，当压力传感器示数为零时，触发速度传感器测出C的速度为v。
（2）在实验中保持A，B质量不变，改变C的质量M，多次重复第（1）步。
①该实验中，M和m大小关系必需满足M _____ m(选填“小于”、“等于”或“大于”)
②为便于研究速度v与质量M的关系，每次测重物的速度时，其已下降的高度应_________(选填“相
同”或“不同”)
③根据所测数据，为得到线性关系图线，应作出________(选填“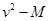”、“”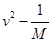或“”)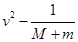
图线。
④根据③问的图线知，图线在纵轴上截距为b，则弹簧的劲度系数为__________（用题给的已知量表
示）。

下图中，固定的光滑竖直杆上套有一质量为m的圆环，圆环与水平放置轻质弹簧一端相连，弹簧另一端固定在墙壁上的A点，图中弹簧水平时恰好处于原长状态。现让圆环从图示位置（距地面高度为h）由静止沿杆滑下，滑到杆的底端B时速度恰好为零。则在圆环下滑至底端的过程中

A．圆环的机械能守恒

B．弹力对圆环做负功，大小为mgh

C．圆环所受合力做功为零

D．圆环到达B时弹簧弹性势能为mgh

如图所示，质量相等物体A、B处于静止状态，此时物体B刚好与地面接触，现剪断绳子OA，下列说法正确的是（     ）

A．剪断绳子的瞬间，物体A的加速度为，物体B的加速度为0
B．弹簧恢复原长时，物体A的动能最大
C．当弹簧压缩到最短时，物体B对地面压力最大
D．剪断绳子后，物体A的机械能守恒