两个劲度系数分别为
和
的轻质弹簧
、
串接在一起，弹簧的一端固定在墙上，如图所示. 开始时两弹簧均处于原长状态，现用水平力作用在弹簧的
端向右拉动弹簧，已知弹的伸长量为
，则弹簧的伸长量为 .
电梯内的水平地板上，竖直放置一根轻质弹簧，弹簧上端固定质量为m的物体。当电梯沿竖直方向匀速运动时，弹簧被压缩了x；当电梯接着做减速运动时，弹簧又被继续压缩了0.1x。重力加速度大小为g。则弹簧的劲度系数k=________；该电梯做匀速运动时的速度方向为_________，电梯做减速运动时的加速度大小是________。
如图为一轻质弹簧的长度L和弹力f大小的关系,试由图线确定：
(1)弹簧的原长 m；
(2)弹簧的劲度系数 N/m；
(3)弹簧长为0.20m时,弹力的大小 N．
在下列各图中，画出木块或小球受到的弹力的示意图：
木块静止在水平面上
木块静止在斜面上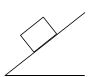 
小球被光滑斜面和光滑挡板夹住静止不动
倒V型支架的底端固定在小车上，另一端固定一个小球，整体静止不动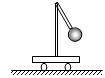
大量事实表明：弹力的大小跟形变的大小有关。某同学为了探究“弹簧的弹力F和弹簧伸长量x的关系”对某一弹簧进行了测试，根据测得的数据绘出了如图所示的图线。这根弹簧在正常使用时的劲度系数为 N/m。
一轻弹簧受到100 N的拉力时，它的长度是11 cm；当它受的拉力再增大50 N，达到150 N时，弹簧长度是13 cm，则弹簧的劲度系数是 N/m，弹簧的原长是 cm.
用金属制成的线材（如纲丝、钢筋）受到的拉力会伸长，17世纪英国物理学家胡克发现，金属丝或金属杆在弹性限度内的伸长与拉力成正比，这就是著名的胡克定律．这个发现为后人对材料的研究奠定了重要的基础．现有一根用新材料制成的金属杆，长为4m，横截面积为0.8 cm2，设计要求它受到拉力后的伸长不超过原长的1/1 000,由于这一拉力很大，杆又较长，直接测试有困难，就选用同种材料制成样品进行测试，通过测试取得数据如下：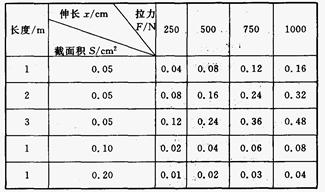
(1)根据测试结果，推导出线材伸长x与材料的长度L、材料的横截面积S及拉力F的函数关系为 。
(2)在寻找上述关系中，你运用哪种科学研究方法？ 。
(3)通过对样品的测试，求出新材料制成的金属细杆能承受的最大拉力约 。
如图2所示，劲度系数分别为k1=30N/m,k2=50N/m轻弹簧竖直挂着，两弹簧之间有一质量为m1=2kg重物，最下端挂一质量为m2=4kg重物，现用力F竖直向上托起m2，当力F为 N 时，两弹簧总长等于两弹簧原长之和。（取g=10m/s2）
某弹簧原长10cm，如果在它的下端挂60N的重物时弹簧的长度变为12cm。当它缩短1.5cm时产生的弹力是 N,当它受到75N的拉力时，它应伸长 cm。（在弹性限度内 ）
如图所示，重力G＝100N的物体置于水平面上，给物体施加一个与水平面成
的拉力F，F＝20N，受到力F作用后物体仍然处于静止状态．物体受到的支持力为 N．物体受到的摩擦力为 N．
一根弹簧在弹性限度内，对其施加30N的拉力时，其长度为20cm，对其施30N压力时，其长度为14cm，则该弹簧自然长度为 cm，其劲度系数为 N/m。
如图所示，在光滑的水平地面上，有两个质量相等的物体，中间用劲度系数为k的轻质弹簧相连，在外力作用下运动，已知F1>F2，当运动达到稳定时，弹簧的伸长量为________
试题篮
()
粤公网安备 44130202000953号
