高中物理探究向心力大小与半径、角速度、质量的关系选择题

如图所示，将一个小球用细线悬挂起来，让小球在a、b之间来回摆动，c点为小球圆弧轨迹的最低点，则以下说法中正确的是

A．小球做简谐振动的回复力是摆球重力沿圆弧线方向的分力

B．小球由c到b的过程，动能减小，重力势能增大

C．小球在c点时的重力势能最大， 向心加速度也最大

D．在平衡位置时，摆线张力最大，回复力也最大

如图所示，两根相互垂直的细线把质量为m的小球悬挂在图示P位置并保持静止，这时沿OP方向的细线与竖直方向的夹角为θ，细线中的拉力大小为F_TP；现在剪断细线NP，当小球摆到位置Q(图中未画出)时，OQ与竖直方向夹角也为θ。下列说法正确的是

A．剪断细线NP的瞬间，小球处于平衡状态

B．剪断细线NP前、后的瞬间，细线OP中的拉力都为FTP=mgcosθ

C．小球在Q点时的加速度为重力加速度g

D．小球运动到最低点时处于超重状态

如图所示，用不可伸长的轻线悬挂在同一点的A、B两个相同小球，让它们在不同高度的水平面内做半径相同的匀速圆周运动，则

A．A的角速度小于B的角速度
B．A的向心加速度小于B的向心加速度
C．A的线速度小于B的线速度
D．A的周期小于B的周期

如图,竖直环A半径为r，固定在木板B上，木板B放在水平 地面上，B的左右两侧各有一档板固定在地上，B不能左右运动，在环的最低点静放有一小球C，A．B．C的质量均为m。给小球一水平向右的瞬时速度v，小球会在环内侧做圆周运动，为保证小球能通过环的最高点，且不会使环在竖直方向上跳起，（不计小球与环的摩擦阻力），最大瞬时速度v为  （   ）

A．           B．           C．           D．

如图所示，一个内壁光滑的圆管轨道ABC竖直放置，轨道半径为R．O、A、D位于同一水平线上，A、D间的距离为R．质量为m的小球（球的直径略小于圆管直径），从管口A正上方由静止释放，要使小球能通过C点落到AD区，则球经过C点时（ ）

A．速度大小满足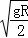≤v_c≤
B．速度大小满足0≤v_c≤
C．对管的作用力大小满足mg≤F_C≤mg
D．对管的作用力大小满足0≤F_c≤mg

如图所示，长度为l的细线，一端固定于O点，另一端拴一小球，先将线拉直呈水平，使小球位于P点，然后无初速释放小球，当小球运动到最低点时，悬线遇到在O点正下方水平固定着的钉子K，不计任何阻力，若要求小球能绕钉子在竖直面内做完整圆周运动，则K与O点的距离可以是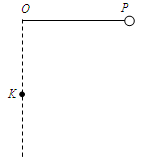

A．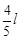

B．

C．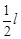

D．

如图所示，竖直平面内固定有一个半径为R的光滑圆弧轨道，其端点P在圆心0的正上方，另一个端点Q与圆心0在同一水平面上．一只小球（视为质点）从Q点正上方某一高度处自由下落．为使小球从Q点进入圆弧轨道后从P点飞出，且恰好又从Q点进入圆弧轨道，小球开始下落时的位置到P点的高度差h应该是   （ ）

A．R

B．R/4

C．3R/2

D．无论h是多大都不可能

如图所示，甲、乙两水平圆盘紧靠在一块，甲圆盘为主动轮，乙靠摩擦随甲无打滑转动．甲圆盘与乙圆盘的半径之比为r_甲∶r_乙＝2∶1，两圆盘和小物体m₁、m₂之间的动摩擦因数相同，m₁距O点为2r，m₂距O′点为r，当甲缓慢转动起来且转速慢慢增加时（ ）．

A．与圆盘相对滑动前m1与m2的角速度之比ω1∶ω2＝2∶1

B．与圆盘相对滑动前m1与m2的向心加速度之比a1∶a2＝1∶2

C．随转速慢慢增加，m1先开始滑动

D．随转速慢慢增加，m2先开始滑动

一杂技演员骑摩托车沿一竖直圆形轨道做特技表演，如图所示．A、C两点分别是轨道的最低点和最高点，B、D分别为两侧的端点， 若运动中速率保持不变，人与车的总质量为m，设演员在轨道内逆时针运动．下列说法正确的是（ ）

A．人和车的向心加速度大小不变
B．摩托车通过最低点A时，轨道受到的压力可能等于mg
C．由D点到A点的过程中，人始终处于超重状态
D．摩托车通过A、C两点时，轨道受到的压力完全相同

如图所示，一个内壁光滑的圆锥形筒的轴线垂直于水平面，圆锥筒固定，有质量相等的小球A和B沿着筒的内壁在水平面内作匀速圆周运动，A的运动半径较大，则下列说法正确的是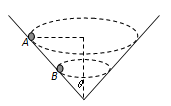

A．球A的线速度小于球B的线速度

B．球A的角速度大于球B的角速度

C．球A的加速度等于球B的加速度

D．球A对筒壁的压力大小大于球B对筒壁的压力大小

如图所示，细绳的一端固定在O点，另一端系一质量为m的小球(可视为质点)，当小球在竖直平面内沿逆时针方向做圆周运动时，通过传感器测得轻绳拉力F_T与轻绳与竖直方向OP的夹角θ满足关系式F_T＝a＋bcos θ，式中a、b为常数。若不计空气阻力，则当地的重力加速度为(  )

A．

B．

C．

D．

赤道上随地球自转的物体A，赤道上空的近地卫星B，地球的同步卫星C，它们的运动都可以视为匀速圆周运动．分别用a、v、T、ω表示物体的向心加速度、速度、周期和角速度，下列判断正确的是（ ）

A．aA＞aB＞aC

B．vB＞vC＞vA

C．TA＞TB＞TC

D．ωA＞ωC＞ωB

人类向宇宙空间发展最具可能的是在太阳系内地球附近建立“太空城”。设想中的一个圆柱形太空城，其外壳为金属材料，长，直径，内壁沿纵向分隔成6个部分，窗口和人造陆地交错分布，陆地上覆盖厚的土壤，窗口外有巨大的铝制反射镜，可调节阳光的射入，城内部充满空气、太空城内的空气、水和土壤最初可从地球和月球运送，以后则在太空城内形成与地球相同的生态环境。为了使太空城内的居民能如地球上一样具有“重力”，以适应人类在地球上的行为习惯，太空城将在电力的驱动下，绕自己的中心轴以一定的角速度转动。如图为太空城垂直中心轴的截面，以下说法正确的有

A．太空城内物体所受的“重力”一定通过垂直中心轴截面的圆心

B．人随太空城自转所需的向心力由人造陆地对人的支持力提供

C．太空城内的居民不能运用天平准确测出质量

D．太空城绕自己的中心轴转动的角速度越大，太空城的居民受到的“重力”越大

在一次探究活动中，某同学设计了如图所示的实验装置，将半径R="1" m的光滑半圆弧轨道固定在质量M="0.5" kg、长L="4" m的小车的上表面中点位置，半圆弧轨道下端与小车的上表面水平相切，现让位于轨道最低点的质量m="0.1" kg的光滑小球随同小车一起沿光滑水平面向右做匀速直线运动，某时刻小车碰到障碍物而瞬时处于静止状态（小车不反弹），之后小球离开圆弧轨道最高点并恰好落在小车的左端边沿处，该同学通过这次实验得到了如下结论，其中正确的是（g取10 m/s²） (  )

A．小球到达最高点的速度为m/s

B．小车与障碍物碰撞时损失的机械能为12.5 J

C．小车瞬时静止前、后，小球在轨道最低点对轨道的压力由1 N瞬时变为6.5 N

D．小车向右做匀速直线运动的速度约为6.5 m/s

一质点以匀速率做曲线运动，从右图所示的轨迹可知，质点加速度最大的点是（    ）

A．A点

B．B点

C．C点

D．D点