高中物理探究向心力大小与半径、角速度、质量的关系计算题

有一个竖直放置的圆形轨道，半径为R，由左右两部分组成。如图所示，右半部分AEB是光滑的半圆轨道，左半部分BFA是粗糙的半圆管轨道．现在最低点A给一个质量为m的小球一个水平向右的初速度，使小球沿轨道恰好运动到最高点B，小球在B点又能沿BFA轨道回到点A，到达A点时对轨道的压力为4mg．求

（1）小球在A点的初速度V₀
（2）小球由B经F回到A的过程中克服摩擦力所做的功．

如图，置于圆形水平转台边缘的小物块随转台加速转动，当转速达到某一数值时，物块恰好滑离转台开始做平抛运动。现测得转台半径R = 0.5m,离水平地面的高度H = 0.8m,物块平抛落地过程水平位移的大小S = 0.4m。设物块所受的最大静摩擦力等于滑动摩擦力，取重力加速度g=10m/s²求：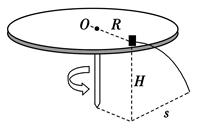

（1）物块做平抛运动的初速度大小V₀；
（2）物块与转台间的动摩擦因数。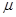

如图所示为一正在匀速行驶的汽车车厢顶部有一根竖直悬挂的不可伸长的轻绳，下端拴一小物块，上端固定在A点且与一能测量绳的拉力的测力传感器相连．已知小物块的质量为5kg, 绳的长度为0.5m，各种阻力都可忽略．若汽车突然停止运动，之后测力传感器测得绳的拉力F随时间t的变化关系如图所示．则根据力学规律和题中（包括图）提供的信息，试求：

（1）汽车在停止前运行的速度v₁；
（2）t₁时刻小球的速度v₂

如图所示，在同一竖直平面内，一轻质弹簧一端固定，另一自由端恰好与水平线AB齐平，静止放于光滑斜面上，一长为L的轻质细线一端固定在O点，另一端系一质量为m的小球，将细线拉至水平，此时小球在位置C，由静止释放小球，小球到达最低点D时，细绳刚好被拉断，D点到AB的距离为h，之后小球在运动过程中恰好沿斜面方向将弹簧压缩，弹簧的最大压缩量为x，重力加速度为g.求：

(1)细绳所能承受的最大拉力；
(2)斜面的倾角θ的正切值；
(3)弹簧所获得的最大弹性势能．

如图所示，光滑水平面AB与竖直面的半圆形导轨在B点衔接，导轨半径R，一个质量为m的静止物块在A处压缩弹簧，把物块释放，在弹力的作用下获得一个向右的速度，当它经过B点进入导轨瞬间对导轨的压力为其重力的7倍，之后向上运动恰能完成半圆周运动到达C点，求：
（1）弹簧对物块的弹力做的功；
（2）物块从B至C克服阻力所做的功；
（3）物块离开C点后落回水平面时动能的大小.

如图所示，小球沿光滑的水平面冲上一个光滑的半圆形轨道，已知轨道的半径为R，小球到达轨道的最高点时对轨道的压力大小恰好等于小球的重力。请求出：

（1）小球到达轨道最高点时的速度为多大；
（2）小球落地时距离A点多远；落地时速度多大？

在航天事业中要用角速度计可测得航天器自转的角速度ω，其结构如图9所示，当系统绕OO′转动时，元件A在光滑杆上发生滑动，并输出电信号成为航天器的制导信号源。已知A质量为m，弹簧的劲度系数为k，原长为L₀，电源电动势为E，内阻不计，滑动变阻器总长为L，电阻分布均匀，系统静止时滑动变阻器触头P在中点，与固定接头Q正对，当系统以角速度ω转动时，求：

（1）弹簧形变量x与ω的关系式；
（2）电压表的示数U与角速度ω的关系式

如图所示，轨道ABCD的AB段为一半径R=0.2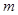的光滑1/4圆形轨道，BC段为高为h=5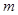的竖直轨道，CD段为水平轨道。一质量为0.1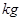的小球由A点从静止开始下滑到B点时速度的大小为2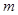/s，离开B点做平抛运动，求：
（1）小球离开B点后，在CD轨道上的落地点到C的水平距离；
（2）小球到达B点时对圆形轨道的压力大小？
（3）如果在BCD轨道上放置一个倾角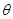＝45°的斜面（如图中虚线所示），那么小球离开B点后能否落到斜面上？如果能，求它第一次落在斜面上的位置。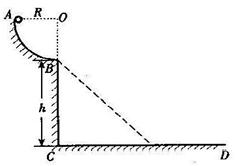

如图，小球做匀速圆周运动，细线与竖直方向夹角为，线长为L，小球质量为m，重力加速度为g．求：(1)绳子对小球的拉力的大小；
(2)小球运动的向心加速度大小；  (3)小球运动的周期．

如图甲所示，竖直平面内的坐标系xoy内的光滑轨道由半圆轨道OBD和抛物线轨道OA组成，OBD和OA相切于坐标原点O点，半圆轨道的半径为R , 一质量为m的小球（可视为质点）从OA轨道上高H处的某点由静止滑下。（1）若小球从H=3R的高度静止滑下，求小球刚过O点时小球对轨道的压力；

（2）若用力传感器测出滑块经过圆轨道最高点D时对轨道的压力为F，并得到如图乙所示的压力F与高度H的关系图象，取g=10m/s²。求滑块的质量m和圆轨道的半径R的值。

质量为m的球用长为L的细绳悬于天花板的O点，并使之在水平面内做匀速圆周运动，细线与竖直线成θ角，求

（1）画出小球的受力示意图
（2）小球做匀速圆周运动线速度的大小

如图所示，一半径R=1m的圆盘水平放置，在其边缘 E点固定一小桶(可视为质点)。在圆盘直径 DE 的正上方平行放置一水平滑道 BC ，滑道右端 C点 与圆盘圆心O在同一竖直线上，且竖直高度 h =" 1.25" m。AB为一竖直面内的光滑四分之一圆弧轨道，半径r=0.45m，且与水平滑道相切与B点。一质量m=0.2kg的滑块（可视为质点）从A点由静止释放，当滑块经过B点时，圆盘从图示位置以一定的角速度ω绕通过圆心的竖直轴匀速转动，最终物块由C点水平抛出，恰好落入圆盘边缘的小桶内．已知滑块与滑道 BC间的摩擦因数＝0.2。（取g=10m/）

求
（1）滑块到达B点时对轨道的压力
（2）水平滑道 BC的长度；
（3）圆盘转动的角速度ω应满足的条件。

如图所示，半径为R=1m的光滑半圆轨道CD竖直放置，与粗糙水平面相切于C点。质量为=10kg的滑块在与水平方向成=37⁰的恒力作用下，从A点由静止开始运动，前进到B点后撤掉力。小物块继续前进经过C点进入半圆轨道，恰能通过最高点D。若恒力大小为100N，且AC段长为10.5m，动摩擦因数为=0.2。求：AB间的距离为多少？（sin37⁰="0.6"   g=10m／s²）

质量m=1kg的小球在长为L=1m的细绳作用下在竖直平面内做圆周运动，细绳能承受的最大拉力T_max=46N，转轴离地h=6m，在某次运动中，在最低点时细绳恰好被拉断。（取g=10m/s²）求：

（1）绳断时小球的速度；
（2）绳断后小球在水平方向上的位移。

一根长l=0.625m的细绳，一端栓一质量m=0.4kg的小球，使其在竖直平面内绕绳的另一端做圆周运动，求：
（1）小球通过最高点是的最小速度；
（2）若小球以速度v=3.0m/s通过圆周最高点时，绳对小球的拉力多大？若此时绳突然断了，小球将如何运动？