如图所示,质量为 ,带电量为
,带电量为 的小球,在P点具有沿PQ方向的初速度
的小球,在P点具有沿PQ方向的初速度 ,为使小球能沿PQ方向运动,施加一垂直于PQ沿斜向左上方的匀强电场,求:(1)所加电场的电场强度为多大?(2)小球经多长时间回到P点?
,为使小球能沿PQ方向运动,施加一垂直于PQ沿斜向左上方的匀强电场,求:(1)所加电场的电场强度为多大?(2)小球经多长时间回到P点?
右图是有两个量程的电流表,当使用A.b两个端点时,量程为1A.当使用A.c两个端点时,量程为0.1A.已知电流表的内阻Rg为200Ω,满偏电流Ig为2mA,求电阻R1、R2的值.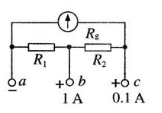
真空中存在空间范围足够大的、水平向右的匀强电场。在电场中,若将一个质量为m、带正电的小球由静止释放,运动中小球的速度与竖直方向夹角为37°(取sin37°="0.6," cos37°=0.8)。现将该小球从电场中某点以初速度υ0竖直向上抛出。求运动过程中
(1)小球受到的电场力的大小及方向;
(2)小球从抛出点至最高点的电势能变化量;
(3)小球再回到与抛出点同一水平面时距离抛出点多远;
如图17所示,交流发电机电动势的有效值E=30 V,内阻不计,它通过一个R=6 Ω的指示灯连接降压变压器.变压器输出端并联96只彩色小灯泡,每只灯泡都是“6 V,0.25 W”,灯泡都正常发光,导线电阻不计.求:
(1)指示灯上的电压;
(2)发电机的输出功率.
如图所示,一带电量为-q、质量为m的粒子以初速度v0从两平行板电容器中央水平射入,从离上板为 d处飞离平行板,若平行板长为l,两板距离为d,(不计粒子重力)则:(1)两板所加电压多大?(2)飞离平行板时带电粒子速度多大?
d处飞离平行板,若平行板长为l,两板距离为d,(不计粒子重力)则:(1)两板所加电压多大?(2)飞离平行板时带电粒子速度多大?
某电站的输出功率为104 kw,输出电压为4kV,通过理想变压器向远处供电,已知输电线总电阻为25.6Ω,输电效率为96%,求:
(1)升压变压器原副线圈匝数之比
(2)输电线上的电压损失
一根长为l的丝线吊着一质量为m的带电量为q的小球静止在水平向右的匀强电场中,如图所示,丝线与竖直方向成37o角,现突然将该电场方向变为向下且大小不变,不考虑因电场的改变而带来的其他影响,(重力加速度为g),求:
(1)匀强电场的电场强度的大小;
(2)求小球经过最低点时丝线的拉力.
面积S = 0.2m2、n = 100匝的圆形线圈,处在如图所示的磁场内(线圈右边的电路中没有磁场),磁感应强度随时间t变化的规律是B = 0.02t,R = 3Ω,C = 30μF,线圈电阻r = 1Ω,求:
(1)通过R的电流大小
(2)电容器的电荷量。
发电机输出功率为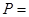 100 kW,输出电压是
100 kW,输出电压是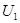 ="250" V,用户需要的电压是
="250" V,用户需要的电压是 220 V,输电线电阻为
220 V,输电线电阻为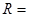 10 Ω.若输电线中因发热而损失的功率为输送功率的4%,试求在输电线路中设置的升、降压变压器原副线圈的匝数比.
10 Ω.若输电线中因发热而损失的功率为输送功率的4%,试求在输电线路中设置的升、降压变压器原副线圈的匝数比.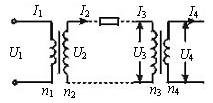
某交流发电机输出功率为5×105W,输出电压为U1=1.0×103V,假如输电线的总电阻R=10Ω,在输电线上损失的电功率等于输电功率的5%,用户使用电压U4=380V.所用升压和降压变压器的原、副线圈的匝数比是多少?(使用的变压器是理想变压器)
图甲左侧的调压装置可视为理想变压器,负载电路中R=55Ω,两电表为理想电流表和电压表,变压器原副线圈匝数比为n1:n2=2:1,若原线圈接入如图乙所示的正弦交变电压。求:
(1)交流电压的函数表达式;
(2)电流表的示数I。
24.(15分)材料的电阻率ρ随温度变化的规律为ρ=ρ0(1+at),其中α称为电阻温度系数,ρ0是材料在t="0" ℃时的电阻率.在一定的温度范围内α是与温度无关的常数。金属的电阻一般随温度的增加而增加,具有正温度系数;而某些非金属如碳等则相反,具有负温数系数.利用具有正负温度系数的两种材料的互补特性,可制成阻值在一定温度范围内不随温度变化的电阻.已知:在0 ℃时,铜的电阻率为1.7×10 –8Ω•m,碳的电阻率为3.5×10 -5Ω•m,附近,在0 ℃时,.铜的电阻温度系数为3.9×10 –3 ℃-1,碳的电阻温度系数为-5.0×10-4℃-1.将横截面积相同的碳棒与铜棒串接成长1.0 m的导体,要求其电阻在0 ℃附近不随温度变化,求所需碳棒的长度(忽略碳棒和铜棒的尺寸随温度的变化).
试题篮
()