高中物理用描迹法画出电场中平面上的等势线计算题

S为一离子源，它能机会均等地向ＭＮ右方空间各方向持续地大量发射相同的正离子。.离子质量为m=1×10^-15kg，电量为q=2×10^-8C ，速度为v₀=4×10⁵m/s。在S右侧有一半径为R=4×10^-2m的圆屏，OO′是过其圆心且垂直圆面的中心轴线。（不考虑离子的重力和离子之间的碰撞效应）：如果S与圆屏间有范围足够大的电场强度为E=5×10⁶V/m的匀强电场，方向垂直屏向右．S发射的所有离子，都能打到屏上。求S与屏的最大距离。

(18分)1897年汤姆逊发现电子后，许多科学家为测量电子的电荷量做了大量的探索。1907-1916年密立根用带电油滴进行实验，发现油滴所带的电荷量是某一数值的整数倍，于是称这数值为基本电荷。
如图所示，完全相同的两块金属板正对着水平放置，板间距离为。当质量为的微小带电油滴在两板间运动时，所受空气阻力的大小与速度大小成正比。两板间不加电压时，可以观察到油滴竖直向下做匀速运动，通过某一段距离所用时间为；当两板间加电压(上极板的电势高)时，可以观察到同一油滴竖直向上做匀速运动，且在时间内运动的距离与在时间内运动的距离相等。忽略空气浮力。重力加速度为。

（1）判断上述油滴的电性，要求说明理由；
（2）求上述油滴所带的电荷量；
（3）在极板间照射X射线可以改变油滴的带电量。再采用上述方法测量油滴的电荷量。如此重复操作，测量出油滴的电荷量如下表所示。如果存在基本电荷，请根据现有数据求出基本电荷的电荷量(保留到小数点后两位)。

实验次序	1	2	3	4	5
电荷量	0.95	1.10	1.41	1.57	2.02

（选做题1）如图所示，用一条绝缘细线悬挂一个带电小球，小球的重力mg=0.1N,带电量q=+2.010⁸C,现加一方向竖直向上的匀强电场，使细线受到的拉力恰好等于零。
求：（1）电场力F；
（2）电场强度E。

(14分)如图所示，电荷量均为q，质量分别为m和2m的小球A和B，中间有细线相连。在电场中以v₀匀速上升。某时刻细线断开，求：（1）电场强度的大小；（2）当B球速度为零时，小球A的速度大小；（3）自绳子断开到B球速度为零的过程中，两球机械能的增量。

图中虚线MN是一垂直纸面的平面与纸面的交线，在平面右侧的半空间存在一磁感强度为B的匀强磁场，方向垂直纸面向外。O是MN上的一点，从O点可以向磁场区域发射电量为+q、质量为m、速率为v的粒子，粒子射入磁场时的速度可在纸面内各个方向。已知先后射入的两个粒子恰好在磁场中给定的P点相遇，P到O的距离为L。不计重力及粒子间的相互作用。
(1)求所考察的粒子在磁场中的轨道半径。
(2)求这两个粒子从O点射入磁场的时间间隔。

如图，一绝缘细圆环半径为r，环面处于水平面内，场强为E的匀强电场与圆环平面平行。环上穿有一电量为＋q、质量为m的小球，可沿圆环做无摩擦的圆周运动。若小球经A点时速度的方向恰与电场垂直，且圆环与小球间沿水平方向无力的作用（设地球表面重力加速度为g）。则：

（1）小球经过A点时的速度大小v_A是多大？
　（2）当小球运动到与A点对称的B点时，小球的速度是多大？圆环对小球的作用力大小是多少？

如图所示，一条长为的细线，上端固定，下端拴一质量为 m的带电小球，将它置于一匀强电场中，电场强度大小为E，方向水平向右，当细线离开竖直位置的偏角为θ时，小球处于平衡，则小球带何种电荷？小球所带电量为多少？

如图所示，一根光滑绝缘细杆与水平面成的角倾斜固定。细杆的一部分处在场强方向水平向右的匀强电场中，场强E=2×10⁴N／C。在细杆上套有一个带电量为q=－1.73×10⁵C、质量为m=3×10^-2kg的小球。现使小球从细杆的顶端A由静止开始沿杆滑下，并从B点进入电场，小球在电场中滑至最远处的C点。已知AB间距离，g=10m/s²。求：
（1）带电小球在B点的速度v_B；
（2）带电小球进入电场后滑行最大距离x₂；
（3）带电小球从A点滑至C点的时问是多少?

在电场强度为E的匀强电场中，一条与电场线平行的直线上有两个静止的小球A和B (均可看作质点)，两小球的质量均为m，A球带电荷量为+Q，B球不带电。开始时两球相距L，只在电场力的作用下，A球开始沿直线运动，并与B球发生正对碰撞。碰撞中A、B两球的总动能无损失，A、B两球间无电荷转移，重力不计。问：
（1）A球经过多长时间与B球发生第一次碰撞?
（2）第一次碰撞后，A、B两球的速度各为多大?
（3）第一次碰撞后，要经过多长时间再次发生碰撞?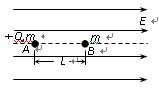

如图所示，均可视为质点的三个物体A、B、C穿在竖直固定的光滑绝缘细线上，A与B紧靠在一起（但不粘连），C紧贴着绝缘地板，质量分别为M_A=2.32kg，M_B=0.20kg，M_C=2.00kg，其中A不带电，B、C的带电量分别为q_B = +4.0×10^-5c，q_C =+7.0×10^-5c，且电量都保持不变，开始时三个物体均静止。现给物体A施加一个竖直向上的力F，若使A由静止开始向上作加速度大小为a=4.0m/s²的匀加速直线运动，则开始需给物体A施加一个竖直向上的变力F，经时间t后，F变为恒力。已知g=10m/s²，静电力恒量k=9×10⁹N·m²/c²，求：

（1）静止时B与C之间的距离；
（2）时间t的大小；
（3）在时间t内，若变力F做的功W_F=53.36J，则B所受的电场力对B做的功为多大？

某研究性学习小组设计了以下方法来测量物体的带电量.如图所示的小球是一个外表面镀有金属膜的空心塑料球，用绝缘丝线悬挂于O点，O点固定一个可测量丝线偏离竖直方向角度的量角器，M、N是两块相同的、正对着平行放置的金属板（加上电压后其内部电场可看作匀强电场）。另外还要用到的器材有天平、刻度尺、电压表、直流电流表、开关、滑动变阻器及导线若干.该小组的实验步骤如下，请你帮助该小组完成：

（1）用天平测出小球的质量，按上图所示进行器材的安装，并用刻度尺测出M、N板之间的距离，使小球带上一定的电量
（2）连接电路（请在图中的虚线框中画出实验所用的电路图，电源、开关已经画出）
（3）闭合开关，调节滑动变阻器滑片的位置，读出多组相应的电压表的示数和丝线的偏转角度.
（4）以电压为纵坐标，以__________为横坐标作出过原点的直线，求出直线的斜率
（5）小球的带电量=__________________.（用、、等物理量表示）