高中物理估测压力锅内水的温度计算题

铁的密度ρ=7.8×10³kg/m³、摩尔质量M=5.6×10^-2kg/mol，阿伏加德罗常数
N_A=6.0×10²³mol^-1。铁原子视为球体，估算铁原子的直径大小。（保留一位有效数字）

铁的密度ρ=7.8×10³kg/m³、摩尔质量M=5.6×10^-2kg/mol，阿伏加德罗常数
N_A=6.0×10²³mol^-1。铁原子视为球体，估算铁原子的直径大小。（保留一位有效数字）

用长度放大600倍的显微镜观察布朗运动．估计放大后的小颗粒(炭粒)体积为0.1×10^－9 m³，碳的密度是2.25×10³ kg/m³，摩尔质量是1.2×10^{－2 kg/mol}，阿伏加德罗常数为6.0×10²³ mol^－1，则该小炭粒含分子数约为多少个？(结果取一位有效数字)

．已知水的密度为ρ＝1.0×10³ kg/m³，水的摩尔质量M＝1.8×10^{－2 kg/mol}，求：(保留两位有效数字，N_A＝6×10²³ mol^－1)
(1)1 cm³的水中有多少个水分子？
(2)水分子的直径有多大？

1 mol铜的质量为63.5 g，铜的密度是8.9×10³ kg/m³，试计算(N_A＝6.02×10²³ mol^－1)
(1)一个铜原子的体积；
(2)假若铜原子为球形，求铜原子的直径；
(3)铜原子的质量．

(1)在课本上粗测油酸分子的大小的实验中，油酸酒精溶液的浓度为每1000mL溶液中有纯油酸1mL，用注射器量得1mL上述溶液有200滴，把一滴该溶液滴入盛水的表面撒有痱子粉的浅盘里，待水面稳定后，测得油酸膜的近似轮廓如图所示，图中正方形小方格的边长为1cm，则每一滴油酸酒精溶液中含有纯油酸的体积是_______mL，油酸膜的面积是______cm²，根据上述数据，估测出油酸分子的直径是____ ____m。

（2）某同学在用油膜法估测分子直径实验中，计算结果明显偏大，可能是由于       。

A．油酸未完全散开

B．油酸中含有大量的酒精

C．计算油膜面积时舍去了所有不足一格的方

D．求每滴体积时，1mL的溶液的滴数多记了10滴

已知某气泡内气体密度为1.29kg/m³，平均摩尔质量为0.029kg/mol。阿伏伽德罗常数N_A=6.02×10²³mol^-1，取气体分子的平均直径为2×10^-10m。若气泡内的气体能完全变成液体，请估算出液体体积与原来气体体积之比。（结果保留一位有效数字）

已知金刚石的密度是ρ=3500kg/m³, 有一小块金刚石, 体积是V=6×10^－8m3, 摩尔质量为M=12×10^{－3 kg/mol}，阿伏伽德罗常数为N_A= 6×10²³/mol，求：
（1）这小块金刚石中含有多少个碳原子? （此问需数据计算）
（2）设想金刚石中碳原子是紧密地堆在一起的球体, 试估算碳原子的直径.（此问只需公式计算即可）．

一滴露水的质量约是9×10^-5g。它含有多少个水分子。（取阿伏伽德罗常数N_A=6.0×10²³mol^-1，水的摩尔质量是18g/mol）

（3-3）
（1）1968年，托雷一坎永号油轮在英吉利海峡触礁，有大约8万吨原油泄漏，污染了英国100多千米的海岸线，使25000只海鸟死亡。石油流入海中，危害极大。在海洋中泄漏m=1t原油可覆盖S=12km²的海面，试估算油膜厚度是原油的分子直径的多少倍？（设原油密度为ρ=0．91×10³kg/m³,保留一位有效数字，分子直径的数量级D=10^-10m）
（2）如图所示，一根足够长的两端开口的粗细均匀的直管，竖直插入很大的水银槽中。有个质量不计的横截面积S=1cm²的活塞A，在管中封闭一段长L=10cm的理想气体。开始时A处于静止状态。现在用力F竖直向上缓慢拉动活塞A，不计管壁对A的摩擦。当F=2N时，A再次静止。设整个过程中环境温度不变，外界大气压p₀=1．0×10⁵Pa（约为75cmHg），求：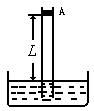

①A再次静止时的气体压强P₂；
②A再次静止时的气体长度L₂；
③在此过程中活塞A上升的距离h。

一种油的密度为，摩尔质量为．取体积为的油慢慢滴出，可滴滴．将其中一滴滴在广阔水面上，形成面积为的单分子油膜。由此可求出：
（1）该油分子的直径；
（2）阿伏加德罗常数；
（3）其中一滴油滴含有的分子数。

在做“用油膜法估测分子的大小”实验中，实验简要步骤如下：

A．将画有油膜轮廓的玻璃板放在坐标纸上，数出轮廓内的方格数（不足半个的舍去，多于半个的算一个）再根据方格的边长求出油膜的面积S.

B．将一滴油酸酒精溶液滴在水面上，待油酸薄膜的形状稳定后，将玻璃板放在浅盘上，用彩笔将薄膜的形状描画在玻璃板上.

C．用浅盘装入约2 cm深的水，然后将痱子粉或石膏粉均匀地撒在水面.

D．用公式D=VS，求出薄膜厚度，即油酸分子的大小.

E.根据油酸酒精溶液的浓度，算出一滴溶液中纯油酸的体积V.
F.用注射器或滴管将事先配制好的油酸酒精溶液一滴一滴地滴入量筒，记下量筒内增加一定体积时的滴数
上述实验步骤的合理顺序是____________________.