如图所示,有一个正方形的匀强磁场区域abcd,e是ad的中点,f是cd的中点,如果在a点沿对角线方向以速度v射入一带负电的带电粒子(带电粒子重力不计),恰好从e点射出,则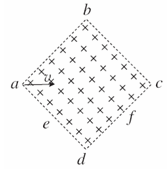
| A.如果粒子的速度增大为原来的二倍,将从d点射出 |
| B.如果粒子的速度增大为原来的三倍,将从f点射出 |
| C.如果粒子的速度不变,磁场的磁感应强度变为原来的二倍,也将从d点射出 |
| D.只改变粒子的速度使其分别从e、d、f点射出时,从e点射出所用时间最短 |
如图(甲)所示,某粒子源向外放射出一个α粒子,粒子速度方向与水平成30°角,质量为m,电荷量为+q。现让其从粒子源射出后沿半径方向射入一个磁感应强度为B、区域为圆形的匀强磁场(区域Ⅰ)。经该磁场偏转后,它恰好能够沿y轴进入下方的平行板电容器,并运动至N板且恰好不会从N板的小孔P射出电容器。已知平行板电容器与一边长为L的正方形单匝导线框相连,其内有垂直框面的磁场(区域Ⅱ),磁场变化如图(乙)所示。不计粒子重力,求:
(1)磁场区域Ⅱ磁场的方向及α粒子射出粒子源的速度大小;
(2)圆形磁场区域的半径;
(3)α粒子在磁场中运动的总时间。
如图是某屏蔽高能粒子辐射的装置,铅盒左侧面中心O有一放射源可通过铅盒右侧面的狭缝MQ向外辐射 粒子,铅盒右侧有一左右边界平行的匀强磁场区域。过O的截面MNPQ位于垂直磁场的平面内,OH垂直于MQ。已知
粒子,铅盒右侧有一左右边界平行的匀强磁场区域。过O的截面MNPQ位于垂直磁场的平面内,OH垂直于MQ。已知 α粒子质量m=6.64×10-27kg,电量q=3.20×10-19C,速率v=1.28×107m/s;磁场的磁感应强度B="0.664" T,方向垂直于纸面向里;粒子重力不计,忽略粒子间的相互作用及相对论效应,sin 530 ="0." 8,cos 530=0.60
α粒子质量m=6.64×10-27kg,电量q=3.20×10-19C,速率v=1.28×107m/s;磁场的磁感应强度B="0.664" T,方向垂直于纸面向里;粒子重力不计,忽略粒子间的相互作用及相对论效应,sin 530 ="0." 8,cos 530=0.60
(1)求垂直于磁场边界向左射出磁场的粒子在磁场中运动的时间t;
(2)若所有粒子均不能从磁场右边界穿出,达到屏蔽作用,求磁场区域的最小宽度d;
(3)求满足(2)条件的所有粒子在磁场中运动的最长时间和最短时间的比值tmax:tmin。
如图所示,等腰直角三角形abc区域中有垂直纸面向里的匀强磁场B,速度为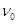 的带电粒子,从a点沿ab方向射入磁场后恰能从c点射出,现将匀强磁场B换成垂直ac边向上的匀强电场E,其它条件不变,结果粒子仍能从c点射出,粒子的重力不计,则下列说法中正确的是
的带电粒子,从a点沿ab方向射入磁场后恰能从c点射出,现将匀强磁场B换成垂直ac边向上的匀强电场E,其它条件不变,结果粒子仍能从c点射出,粒子的重力不计,则下列说法中正确的是
| A.粒子带正电 |
B.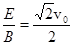 |
| C.粒子从磁场中离开时的速度方向与从电场中离开时的速度方向不同 |
| D.粒子从磁场中离开时的速度大小与从电场中离开时的速度大小不同 |
如图所示,圆形区域内有一垂直纸面的匀强磁场,磁感应强度的大小为B1,P为磁场边界上的一点.相同的带正电荷粒子,以相同的速率从P 点射入磁场区域,速度方向沿位于纸面内的各个方向.这些粒子射出边界的位置均处于边界的某一段弧上,这段圆弧的弧长是圆周长的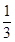 。若将磁感应强度的大小 变为 B2,结果相应的弧长变为圆周长的
。若将磁感应强度的大小 变为 B2,结果相应的弧长变为圆周长的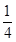 ,不计粒子的重力和粒子间的相互影响,则
,不计粒子的重力和粒子间的相互影响,则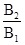 等于
等于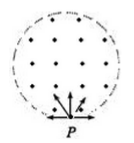
A.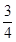 |
B.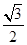 |
C.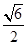 |
D.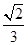 |
(18分)如图所示,在平面直角坐标系中的三角形FGH区域内存在着垂直纸面向里的匀强磁场,磁感应强度大小为B,三点坐标分别为F( -3L,5L)、G( -3L, -3L)、H(5L,-3L)。坐标原点O处有一体积可忽略的粒子发射装置,能够连续不断的在该平面内向各个方向均匀的发射速度大小相等的带正电的同种粒子,单位时间内发射粒子数目稳定。粒子的质量为m,电荷量为q,不计粒子间的相互作用以及粒子的重力。

(1)速率在什么范围内所有粒子均不可能射出该三角形区域?
(2)如果粒子的发射速率为 ,设在时间t内粒子源发射粒子的总个数为N,在FH边上安装一个可以吸收粒子的挡板,那么该时间段内能够打在挡板FH上的粒子有多少?并求出挡板上被粒子打中的长度。
,设在时间t内粒子源发射粒子的总个数为N,在FH边上安装一个可以吸收粒子的挡板,那么该时间段内能够打在挡板FH上的粒子有多少?并求出挡板上被粒子打中的长度。
如图所示,在真空中,半径为R的虚线所围的圆形区域内只存在垂直纸面向外的匀强磁场。有一电荷量为q、质量为m的带正电粒子,以速率V0从圆周上的P点沿垂直于半径OOl并指向圆心O的方向进入磁场,从圆周上的O1点飞出磁场后沿两板的中心线O1O2射入平行金属板M和N, O1O2与磁场区域的圆心O在同一直线上。板间存在匀强电场,两板间的电压为U,两板间距为d。不计粒子所受重力。求:
(1)磁场的磁感应强度B的大小;
(2)粒子在磁场中运动的时间;
(3)粒子在两平行板间运动过程中的最大速度与板长L的关系。
如图所示,平面直角坐标系第一象限存在竖直向上的匀强电场,距离原点O为3a处有一个竖直放置的荧光屏,荧光屏与x轴相交于Q点,且纵贯第四象限。一个顶角等于30°的直角三角形区域内存在垂直平面向里的匀强磁场,三角形区域的一条直角边ML与y轴重合,且ML被x轴垂直平分。已知ML的长度为6a,磁感应强度为B,电子束以相同的速度v0从LO区间垂直y轴和磁场方向射入直角三角形区域。从y=-2a射入磁场的电子运动轨迹恰好经过原点O,假设第一象限的电场强度大小为E=Bv0,试求:
(1)电子的比荷;
(2)电子束从+y轴上射入电场的纵坐标范围;
(3)从磁场中垂直于y轴射入电场的电子打到荧光屏上距Q点的最远距离。
(9分) 如图所示,在空间中存在垂直纸面向外、宽度为d的有界匀强磁场.一质量为m,带电荷量为q的粒子自下边界的P点处以速度v沿与下边界成30°角的方向垂直射入磁场,恰能垂直于上边界射出,不计粒子重力,题中d、m、q、v均为已知量.则:
(1)粒子带何种电荷?
(2)磁场的磁感应强度为多少?
如图所示,半径为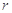 的圆形区域内有垂直纸面向里的匀强磁场,磁感应强度大小为B,磁场边界上A点一粒子源,源源不断地向磁场发射各种方向(均平行于纸面)且速度大小相等的带正电的粒子(重力不计),已知粒子的比荷为
的圆形区域内有垂直纸面向里的匀强磁场,磁感应强度大小为B,磁场边界上A点一粒子源,源源不断地向磁场发射各种方向(均平行于纸面)且速度大小相等的带正电的粒子(重力不计),已知粒子的比荷为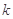 ,速度大小为
,速度大小为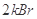 。则粒子在磁场中运动的最长时间为
。则粒子在磁场中运动的最长时间为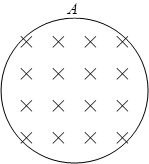
A. |
B.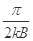 |
C.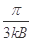 |
D.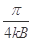 |
如图所示,竖直平面内有一直角坐标系,在y轴的右侧存在无限大的、场强大小为E、水平向左的匀强电场,在y轴的左侧同时存在一个垂直纸面向外、磁感应强度大小为B、水平宽度为a的匀强磁场Ⅰ.有一不计重力、带正电、比荷为 的粒子由+x轴上某一位置无初速度释放.
的粒子由+x轴上某一位置无初速度释放.
(1)若其恰好经过磁场Ⅰ左边界上P点 ,求粒子射出磁场Ⅰ的速度v1的大小;
,求粒子射出磁场Ⅰ的速度v1的大小;
(2)若其恰好经过y轴上的Q点 ,求粒子从释放开始第一次到达Q所用的时间;
,求粒子从释放开始第一次到达Q所用的时间;
(3)若匀强磁场Ⅰ左侧同时存在一个垂直纸面向里、磁感应强度大小也为B的无限大匀强磁场Ⅱ,要使粒子第二次沿+x方向运动时恰经过y轴上的M点 ,试求其在+x轴上无初速度释放时的位置坐标.
,试求其在+x轴上无初速度释放时的位置坐标.
如图所示,在x>O、y>O的空间中有恒定的匀强磁场,磁感应强度的方向垂直于xOy平面向里,大小为B.现有一质量为m、电量为q的带正电粒子,从在x轴上的某点P沿着与x轴成30°角的方向射入磁场。不计重力的影响,则下列有关说法中正确的是
A.粒子在磁场中运动所经历的时间可能为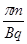
B.粒子在磁场中运动所经历的时间可能为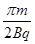
C.只要粒子的速率合适,粒子就可能通过坐标原点
D.粒子一定不可能通过坐标原点
如图所示,以直角三角形AOC为边界的有界匀强磁场区域,磁感应强度为B,∠A=60°,AO=L.在O点放置一个粒子源,可以向各个方向发射某种带负电粒子,粒子的比荷为q/m,发射速度大小都为v0,且满足v0= ,发射方向由图中的角度θ表示.对于粒子进入磁场后的运动(不计重力作用),下列说法正确的是
,发射方向由图中的角度θ表示.对于粒子进入磁场后的运动(不计重力作用),下列说法正确的是
| A.粒子有可能打到A点 |
| B.以θ=60°飞入的粒子在磁场中运动时间最短 |
| C.以θ<30°飞入的粒子在磁场中运动的时间都相等 |
| D.在AC边界上只有一半区域有粒子射出 |
坐标原点O处有一点状的放射源,它向xoy平面内的x轴上方各个方向发射带正电的同种粒子,速度大小都是v0,在0<y<d的区域内分布有指向y轴正方向的匀强电场,场强大小为 ,其中q与m分别为该种粒子的电量和质量;在
,其中q与m分别为该种粒子的电量和质量;在 的区域内分布有垂直于xoy平面的匀强磁场。ab为一块很大的平面感光板,放置于
的区域内分布有垂直于xoy平面的匀强磁场。ab为一块很大的平面感光板,放置于 处,如图所示。观察发现此时恰无粒子打到ab板上。(不考虑粒子的重力)
处,如图所示。观察发现此时恰无粒子打到ab板上。(不考虑粒子的重力)
(1)求粒子刚进入磁场时的动能;
(2)求磁感应强度B的大小;
(3)将ab板平移到什么位置时所有粒子均能打到板上?并求出此时ab板上被粒子打中的区域的长度。
试题篮
()