 (1)子弹的质量
(1)子弹的质量 :
:
(2)小车的位移 时线圈中的电流大小
时线圈中的电流大小 ;
;
(3)在线圈进入磁场的过程中通过线圈某一截面的电荷量 ;
;
(4)线圈和小车通过磁场的过程中线圈电阻产生的热量 。
。

求该镭核在衰变为氡核和x粒子时释放的能量。 (保留三位有效数字,电子电荷量
e="1.60" X 1 0一19 C,lu可近似取1.60 X 10—27 kg) ‘
如下图甲所示,真空中两水平放置的平行金属板C、D,上面分别开有正对的小孔O1和O2,金属板C、D接在正弦交流电源上,C、D两板间的电压UCD随时间t变化的图线如图(乙)所示。t=0时刻开始,从D板小孔O1处连续不断飘入质量为m=3.2×10-25kg、电荷量q=1.6×10-19C的带正电的粒子(设粒子飘入速度很小,可视为零)。在C板外侧有以MN为上边界CM为左边界的匀强磁场,MN与C金属板相距d=10cm,O2C的长度L=10cm,匀强磁场的大小为B=0.1T,方向如图(甲)所示,粒子的重力及粒子间相互作用力不计,平行金属板C、D之间的距离足够小,粒子在两板间的运动时间可忽略不计。求:
(1)带电粒子经小O2进入磁场后,能飞出磁场边界MN的最小速度为多大?
(2)从0到0.04s末时间内哪些时间段飘入小O1的粒子能穿过电场并飞出磁场边界MN。
(3)磁场边界MN有粒子射出的长度范围。(计算结果保留一位有效数字)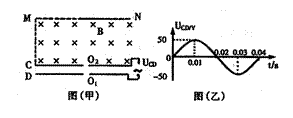
如图所示,在空间存在这样一个磁场区域,以MN为界,上部分的匀强磁场的磁感应强度为B1,下部分的匀强磁场的磁感应强度为B2,B1=2B2=2B0,方向均垂直纸面向内,且磁场区域足够大。在距离界线为h的P点有一带负电荷的离子处于静止状态,某时刻该离子分解成为带电荷的粒子A和不带电的粒子B,粒子A质量为m、带电荷q,以平行于界线MN的速度向右运动,经过界线MN时的速度方向与界线成60°角,进入下部分磁场。当粒子B沿与界线平行的直线到达位置Q点时,恰好又与粒子A相遇。不计粒子的重力。求:
(1)P、Q两点间距离。
(2)粒子B的质量。
如图甲所示,空间有Ⅰ区和Ⅲ区两个有理想边界的匀强磁场区域,磁感应强度大小均为B,方向如图所示。两磁场区域之间有宽度为s的无磁场区域Ⅱ。abcd是由均匀电阻丝做成的边长为L(L>s)的正方形线框,每边的电阻为R。线框以垂直磁场边界的速度v水平向右匀速运动,从Ⅰ区经过Ⅱ区完全进入Ⅲ区,线框ab边始终与磁场边界平行。求:
(1)当ab边在Ⅱ区运动时,dc边所受安培力的大小和方向;
(2)线框从完全在Ⅰ区开始到全部进入Ⅲ区的整个运动过程中产生的焦耳热;
(3)请在图乙的坐标图中画出,从ab边刚进入Ⅱ区,到cd边刚进入Ⅲ区的过程中,
d、a两点间的电势差Uda随时间t变化的图线。其中E0 = BLv。
地球周围有磁场,由太空射来的带电粒子在此磁场中的运动称为磁漂移。以下描述的是一种假设的磁漂移运动。一带正电的粒子在x=0、y=0处沿y方向以某一速度v0运动,空间存在垂直于图中纸面向外的匀强磁场,在y>0的区域中,磁感强度为B1,在y<0的区域中磁感强度为B2,B2>B1,如图所示。
⑴ 把粒子在出发点x=0处作为第0次过x轴,试求粒子到第n次过x轴整个过程中,在x轴方向的平均速度v与v0之比,n只取奇数。
⑵ 若B2:B1= 4,当n很大时,v:v0趋于何值。
如图所示,坐标系xoy位于竖直平面内,在该区域内有场强E=12N/C、方向沿x轴正方向的匀强电场和磁感应强度大小为B =2T,沿水平方向且垂直于xoy平面指向纸里的匀强磁场.一个质量m=4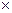 10-5kg,电量q ="2.5"
10-5kg,电量q ="2.5" 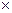 1-5C带正电的微粒,在xoy平面内做匀速直线运动,运动到原点o时,撤去磁场,经一段时间后,带电微粒运动到了x轴上的P点.取g=10 m/s2,求:
1-5C带正电的微粒,在xoy平面内做匀速直线运动,运动到原点o时,撤去磁场,经一段时间后,带电微粒运动到了x轴上的P点.取g=10 m/s2,求:
(1)P点到原点0的距离;
(2)带电微粒由原点0运动到P点的时间.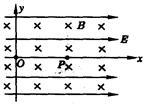
如图所示,真空中两平行金属板A、B长L1=0.10m,间距d= /30m,两极板接在电压UAB=200sinl00πt(V)的交流电源上,与AB板相距L2=0.20m的PS右侧区间有一个范围足够大的匀强磁场,磁场方向垂直纸面向里,磁感应强度为B=
/30m,两极板接在电压UAB=200sinl00πt(V)的交流电源上,与AB板相距L2=0.20m的PS右侧区间有一个范围足够大的匀强磁场,磁场方向垂直纸面向里,磁感应强度为B= ×l0-2T。一束带正电的粒子以Vo=
×l0-2T。一束带正电的粒子以Vo= ×105m/s的速度沿着A,B两极板的中央飞入电场,粒子的比荷q/m=1×l08C/kg,不计粒子的重力和粒子间的相互作用力,不考虑相对论效应。问:
×105m/s的速度沿着A,B两极板的中央飞入电场,粒子的比荷q/m=1×l08C/kg,不计粒子的重力和粒子间的相互作用力,不考虑相对论效应。问:
(1)通过计算说明,带电粒子经过平行金属板期间,加在两板间的电压几乎不变;
(2)在t=0时刻进入电场的粒子,飞离磁场时离O点的距离;
(3)何时进入电场的粒子,从进入电场到离开磁场所经历的时间最长?并计算最长时间。
如图所示,平面坐标系Oxy中,在y>0的区域存在沿y轴负方向的匀强电场,场强大小为E,在-h<y<0的区域Ⅰ中存在垂直纸面向外的匀强磁场,磁感应强度大小为B,在y<-h的区域Ⅱ中存在垂直纸面向里的匀强磁场,磁感应强度大小为2B.A是y轴上的一点, C是x轴上的一点.一质量为m、电荷量为q的带正电的粒子以某一初速度沿x轴正方向从A点进入电场区域,继而通过C点以速度方向与x轴夹角为φ=30°进入磁场区域Ⅰ,并以垂直边界y=-h的速度进入磁场区域Ⅱ.粒子重力不计.试求:(1)粒子经过C点时的速度大小v;
(2)A、C两点与O点间的距离y0、x0;
(3)粒子从A点出发,经过多长时间可回到y=y0处?
如图,在直角坐标系xoy中,点M(0,1)处不断向+y方向发射出大量质量为m、带电量为-q的粒子,粒子的初速度大小广泛分布于零到v0之间。已知这些粒子此后所经磁场的磁感应强度大小为B,方向垂直于纸面向里,所有粒子都以+x方向穿过b区域,都沿-y的方向通过点N(3,0)。
(1)通过计算,求出符合要求的磁场范围的最小面积;
(2)若其中速度为k1v0和k2v0的两个粒子同时到达N点(1>k1>k2>0),求二者发射的时间差。
试题篮
()