一弹簧振子振幅为A,周期为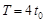 .若振子从平衡位置处开始经过
.若振子从平衡位置处开始经过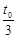 时间时的加速度大小和动能分别为a1和E1,而振子在位移为
时间时的加速度大小和动能分别为a1和E1,而振子在位移为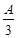 时加速度大小和动能分别为a2和E2,则a1、a2和E1、E2的大小关系为
时加速度大小和动能分别为a2和E2,则a1、a2和E1、E2的大小关系为
| A.a1>a2,E1<E2 | B.a1>a2,E1>E2 |
| C.a1<a2,E1<E2 | D.a1<a2,E1>E2 |
在竖直向下的匀强电场E中,一带电油滴在电场力和重力的作用下,沿虚线所示的运动轨迹从a运动到b.若此带电油滴在运动过程中动能和重力势能之和为E1,重力势能和电势能之和为E2,则E1、E2的变化情况是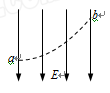
| A.E1增加,E2增加 | B.E1增加,E2减小 |
| C.E1不变,E2减小 | D.E1不变,E2不变 |
如图,质量为M的楔形物A静置在水平地面上,其斜面的倾角为 .斜面上有一质量为m的小物块B,B与斜面之间存在摩擦.用恒力F沿斜面向上拉B,使之匀速上滑.在B运动过程中,楔形物块A始终保持静止.则
.斜面上有一质量为m的小物块B,B与斜面之间存在摩擦.用恒力F沿斜面向上拉B,使之匀速上滑.在B运动过程中,楔形物块A始终保持静止.则
| A.B给A的作用力大小为mg-F |
| B.B给A摩擦力大小为 F |
C.地面受到的摩擦力大小为 Fcos |
D.地面受到的压力大小为Mg+mgcos -Fsin -Fsin |
半径分别为r和2r的两个质量不计的圆盘,共轴固定连结在一起,可以绕水平轴O无摩擦转动,大圆盘的边缘上固定有一个质量为m的质点,小圆盘上绕有细绳.开始时圆盘静止,质点处在水平轴O的正下方位置.现以水平恒力F拉细绳,使两圆盘转动,若两圆盘转过的角度 时,质点m的速度达到最大为vm,此时绳子的速度为vF.则vm与vF、F与mg间的关系是
时,质点m的速度达到最大为vm,此时绳子的速度为vF.则vm与vF、F与mg间的关系是
A. , , |
B. , , |
C. , , |
D. , , |
在离地高h处,以速度v0抛出一小球,不计空气阻力,已知 .则小球落地时间不可能是
.则小球落地时间不可能是
A. |
B. |
C. |
D. |
图示为用“与”门、蜂鸣器等元件组成的简易控制电路.若要让蜂鸣器L鸣叫,则电键S1、S2所处的状态为
| A.S1、S2都闭合 |
| B.S1、S2都断开 |
| C.S1断开,S2闭合 |
| D.S1闭合,S2断开 |
如图,一定质量的理想气体自状态A沿直线变化到状态B的过程中其压强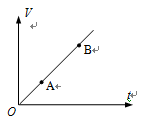
| A.逐渐增大 | B.逐渐减小 |
| C.始终不变 | D.先增大后减小 |
一个弹性小球,在光滑水平面上以5m/s的速度向左垂直撞到墙上,碰撞后小球以大小为3m/s速度向右运动.则碰撞前后小球速度变化量 的大小和方向分别为
的大小和方向分别为
| A.2m/s,向左 | B.2m/s,向右 |
| C.8m/s,向左 | D.8m/s,向右 |
如图所示,A、B为同一水平线上的两个相同的绕绳轮子.现按箭头方向以相同的速度缓慢转动A、B,使重物C缓慢上升.在此过程中绳上的拉力大小

A.保持不变 B.逐渐减小
C.逐渐增大 D.先减小后增大
下列各物理量的表达式中,是用比值法定义该物理量的是
A.加速度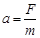 |
B.电功率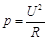 |
C.电场强度 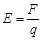 |
D.电流强度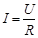 |
从宏观上看,气体分子热运动的平均动能与分子间势能分别取决于气体的
| A.体积和压强 | B.温度和体积 | C.温度和压强 | D.压强和温度 |
物理学史上,正确认识运动和力的关系且推翻“力是维持运动的原因”的物理学家、建立惯性定律的物理学家分别是
| A.亚里士多德 伽利略 | B.亚里士多德 牛顿 |
| C.伽利略 牛顿 | D.伽利略 爱因斯坦 |
太空中存在一些离其它恒星很远的、由三颗星组成的三星系统,可忽略其它星体对它们的引力作用。已观测到稳定的三星系统存在两种基本的构成形式:一种是直线三星系统──三颗星始终在一条直线上;另一种是三角形三星系统──三颗星位于等边三角形的三个顶点上。已知某直线三星系统A 每颗星体的质量均为m,相邻两颗星中心间的距离都为R;某三角形三星系统B 的每颗星体的质量恰好也均为m,且三星系统A 外侧的两颗星作匀速圆周运动的周期和三星系统B 每颗星作匀速圆周运动的周期相等。引力常量为G,则
A.三星系统A 外侧两颗星运动的线速度大小为 |
B.三星系统A 外侧两颗星运动的角速度大小为 |
C.三星系统B 的运动周期为 |
D.三星系统B任意两颗星体中心间的距离为 |
如图所示,以o 点为圆心的圆周上有六个等分点a、b、c、d、e、f。等量正、负点电荷分别放置在a、d 两点时,在圆心o 产生的电场强度大小为E。现仅将放于a 点的正点电荷改放于其他等分点上,使o 点的电场强度改变,则下列判断正确的是
| A.移至c 点时,o 点的电场强度大小仍为E,沿oe 方向 |
B.移至b 点时,o 点的电场强度大小为 ,沿oc 方向 ,沿oc 方向 |
C.移至e 点时,o 点的电场强度大小为 ,沿oc 方向 ,沿oc 方向 |
D.移至f 点时,o 点的电场强度大小为 ,沿oe 方向 ,沿oe 方向 |
一物体由静止开始沿直线运动,其加速度随时间变化的规律如图所示,取物体开始运动的方向为正方向,则下列关于物体运动的v-t 图象正确的是
试题篮
()