如图所示,放置在真空中的三棱镜的横截面为直角三角形ABC,∠A=300,在BC的延长线上有一单色光源S,从S射出的一条光线从AC边上的D点(图中未标出)处射入棱镜中,经三棱镜折射后垂直于AB边射出.若S、D两点的距离为d,且光从光源S到D点的传播时间跟光在三棱镜中传播的时间相等.已知该三棱镜的折射率为 。求:
。求:
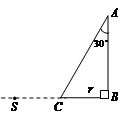
①光线SD射到AC边上的入射角为 ;
②入射点D到顶点A的距离。
(1)下列说法正确的是 ( )
| A.液体表面层分子间距离大于液体内部分子间距离,故液体表面存在张力 |
| B.PM2.5(指空气中直径小于2.5微米的悬浮颗粒物)在空气中的运动属于分子热运动 |
| C.把很多小的单晶体放在一起,就变成了非晶体 |
| D.第二类永动机没有违反能量守恒定律 |
E.水的饱和汽压随温度的升高而增大
F.分子间引力总是随着分子间距离的减小而减小
(2)一端开口的极细玻璃管开口朝下竖直立于水银槽的水银中,初始状态管内外水银面的高度差为l0=62cm,系统温度27℃。因怀疑玻璃管液面上方存在空气,现从初始状态分别进行两次试验如下:
保持系统温度不变,将玻璃管竖直向上提升 (开口仍在水银槽液面以下),结果液面高度差增加
(开口仍在水银槽液面以下),结果液面高度差增加 ;将系统温度升到77℃,结果液面高度差减小
;将系统温度升到77℃,结果液面高度差减小 。已知玻璃管内粗细均匀,空气可看成理想气体,热力学零度可认为为-273℃。求:
。已知玻璃管内粗细均匀,空气可看成理想气体,热力学零度可认为为-273℃。求:
①实际大气压为多少cmHg?
②初始状态玻璃管内的空气柱有多长?
如图l所示,导热性能良好的气缸放置在水平平台上,活塞质量为10 kg,横截面积50 cm2,厚度l cm,气缸全长25 cm,气缸质量20 kg,大气压强为1×105Pa,当温度为17℃时,活塞封闭的气柱长10 cm。现在用一条细绳一端连接在活塞上,另一端通过两个光滑的定滑轮后连接在一个小桶上,如图2所示。开始时活塞静止。现不断向小桶中添加细沙,使活塞缓慢向上移动(g取l0m/s2) 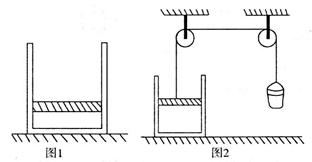
①通过计算判断气缸能否离开台面。
②活塞缓慢向上移动过程中,气缸内气体是________(填“吸热”或放热“),气体的内能__________(填“增加”或“减少”或“不变”)
如图所示,△ABC为一直角三棱镜的截面,其顶角为θ=30°。P为垂直于直线BCD的光屏,现一宽度等于AB的单色平行光束垂直射向AB面,在屏P上形成一条宽度等于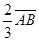 的光带,试作出光路图并求棱镜的折射率。(其中AC的右方存在有折射率为在的透明介质)
的光带,试作出光路图并求棱镜的折射率。(其中AC的右方存在有折射率为在的透明介质)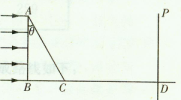
如图所示,在MN的下方足够大的空间是玻璃介质,其折射率为n= ,玻璃介质的上边界MN是屏幕。玻璃中有一正三角形空气泡,其边长l=40 cm,顶点与屏幕接触于C点,底边AB与屏幕平行。激光a垂直于AB边射向AC边的中点O,结果在屏幕MN上出现两个光斑。
,玻璃介质的上边界MN是屏幕。玻璃中有一正三角形空气泡,其边长l=40 cm,顶点与屏幕接触于C点,底边AB与屏幕平行。激光a垂直于AB边射向AC边的中点O,结果在屏幕MN上出现两个光斑。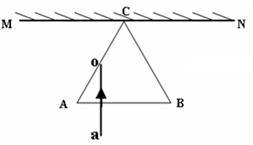
①画出光路图。
②求两个光斑之间的距离L。
一个同学要研究轻质弹簧的弹性势能与弹簧长度改变量的关系,进行了如下实验:在离地面高度为h的光滑水平桌面上,沿着与桌子边缘垂直的方向放置一轻质弹簧,其左端固定,右端与质量为m的一个小钢球接触.当弹簧处于自然长度时,小钢球恰好在桌子边缘,如图所示.让钢球向左压缩弹簧一段距离后由静止释放,使钢球沿水平方向射出桌面,小钢球在空中飞行后落在水平地面上,水平距离为s. 
(1)请你推导出弹簧的弹性势能Ep与小钢球质量m、桌面离地面高度h、小钢球飞行的水平距离s等物理量之间的关系式: .
(2)弹簧的压缩量x与对应的钢球在空中飞行的水平距离s的实验数据如下表所示:
| 弹簧的压缩量x (cm) |
1.00 |
1.50 |
2.00 |
2.50 |
3.00 |
3.50 |
| 小钢球飞行的水平距离s (cm) |
1.01 |
1.50 |
2.01 |
2.49 |
3.01 |
3.50 |
根据上面的实验数据,请你猜测弹簧的弹性势能Ep与弹簧的压缩量x之间的关系为 ,并说明理由: .
1919年,卢瑟福用α粒子轰击氮核发现质子.科学研究表明其核反应过程是:α粒子轰击静止的氮核后形成了不稳定的复核,复核发生衰变放出质子,变成氧核.设α粒子质量为m1,初速度为v0,氮核质量为m2,质子质量为m0,氧核的质量为m3,不考虑相对论效应.
①写出卢瑟福发现质子的核反应方程_
②α粒子轰击氮核形成不稳定复核的瞬间,复核的速度为多大?
③求此过程中释放的核能.
如图所示,透明介质球球心位于O,半径为R,光线DC平行于直径AOB射到介质球的C点,DC与AB的距离H=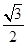 R,若DC光线进入介质球后经一次反射再次回到介质球的界面时,从球内折射出的光线与入射光线平行,作出光路图,并计算出介质的折射率.
R,若DC光线进入介质球后经一次反射再次回到介质球的界面时,从球内折射出的光线与入射光线平行,作出光路图,并计算出介质的折射率.
如图所示为用某种透明材料制成的一块柱形棱镜的截面图,圆弧CD为半径为R的四分之一的圆周,圆心为O,光线从AB面上的某点入射,入射角 ,它进入棱镜后恰好以临界角射在BC面上的O点。
,它进入棱镜后恰好以临界角射在BC面上的O点。
(a)画出光线由AB面进入棱镜且从CD弧面射出的光路图;
(b)求该棱镜的折射率n;
(c)求光线在该棱镜中传播的速度大小(已知光在空气中的传播速度c=3.0×108m/s)。
如图所示是透明圆柱形介质的横截面,BC为圆的直径。一束单色光沿AB方向入射, ABC=120o。光自B点进入介质内只经过一次折射后从介质中射出,出射光线平行于BC。
ABC=120o。光自B点进入介质内只经过一次折射后从介质中射出,出射光线平行于BC。

①求介质的折射率;
②若改变 ABC的大小,则从B点射入介质中的单色光能否在介质的内表面发生全反射?答: (填“能”或“不能”)
ABC的大小,则从B点射入介质中的单色光能否在介质的内表面发生全反射?答: (填“能”或“不能”)
(1)如图甲所示,在某一均匀介质中,A、B是振动情况完全相同的两个波源,其简谐运动表达式均为 ,介质中P点与A、B两波源间的距离分别为4m和5m,两波源形成的简谐波分别沿AP、BP方向传播,波速都是10m/s。
,介质中P点与A、B两波源间的距离分别为4m和5m,两波源形成的简谐波分别沿AP、BP方向传播,波速都是10m/s。

①求简谐横波的波长。
②P点的振动 (填“加强”或“减弱”)。
(2)如图乙所示,ABCD是一直角梯形棱镜的横截面,位于截面所在平面内的一束光线由O点垂直AD边射入。已知棱镜的折射率 ,AB=BC=8cm,OA=2cm,∠OAB=60°。
,AB=BC=8cm,OA=2cm,∠OAB=60°。
①求光线第一次射出棱镜时,出射光线的方向。
②第一次的出射点距C cm。
(1)如图所示的装置,弹簧振子的固有频率是4 Hz. 现匀速转动把手,给弹簧振子以周期性的驱动力,测得弹簧振子振动达到稳定时的频率为1Hz,则把手转动的频率为_______.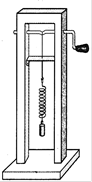
A.1 Hz
B.3 Hz
C.4 Hz
D.5 Hz
(2)如图所示,两艘飞船A、B 沿同一直线同向飞行,相对地面的速度均为v(v 接近光速c). 地面上测得它们相距为L,则A 测得两飞船间的距离_______ (选填“大于”、“等于”或“小于”)L. 当B 向A 发出一光信号,A 测得该信号的速度为_______.
(3)如图为单反照相机取景器的示意图,ABCDE为五棱镜的一个截面,AB BC. 光线垂直AB 射入,分别在CD 和EA 上发生反射,且两次反射的入射角相等,最后光线垂直BC 射出.若两次反射都为全反射,则该五棱镜折射率的最小值是多少?(计算结果可用三角函数表示)
BC. 光线垂直AB 射入,分别在CD 和EA 上发生反射,且两次反射的入射角相等,最后光线垂直BC 射出.若两次反射都为全反射,则该五棱镜折射率的最小值是多少?(计算结果可用三角函数表示)
1801年,托马斯·杨用双缝干涉实验研究了光波的性质.1834年,洛埃利用平面镜同样得到了杨氏干涉的结果(称洛埃镜实验).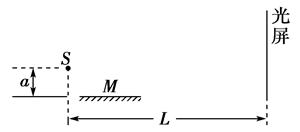
(1)洛埃镜实验的基本装置如图所示,S为单色光源,M为一平面镜.试用平面镜成像作图法画出S经平面镜反射后的光与直接发出的光在光屏上相交的区域.
(2)设光源S到平面镜的垂直距离和到光屏的垂直距离分别为a和L,光的波长为λ,在光屏上形成干涉条纹.写出相邻两条亮纹(或暗纹)间距离Δx的表达式.
(1)以下说法正确的是 。
a.水的饱和汽压随温度的升高而增大
b.扩散现象表明,分子在永不停息地运动
c.当分子间距离增大时,分子间引力增大,分子间斥力减小
d.一定质量的理想气体,在等压膨胀过程中,气体分子的平均动能减小
(2)如图所示,粗细均匀、导热良好、装有适量水银的U型管竖直放置,右端与大气相通,左端封闭气柱长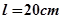 (可视为理想气体),两管中水银面等高。先将右端与一低压舱(未画出)接通,稳定后右管水银面高出左管水银面
(可视为理想气体),两管中水银面等高。先将右端与一低压舱(未画出)接通,稳定后右管水银面高出左管水银面 (环境温度不变,大气压强
(环境温度不变,大气压强 )
)
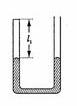
①求稳定后低压舱内的压强(用“cmHg”做单位)
②此过程中左管内的气体对外界 (填“做正功”“做负功”“不做功”),气体将 (填“吸热”或放热“)。
(1)下列现象中,能说明液体存在表面张力的有 _________.
(A) 水黾可以停在水面上
(B) 叶面上的露珠呈球形
(C) 滴入水中的红墨水很快散开
(D) 悬浮在水中的花粉做无规则运动
(2)密闭在钢瓶中的理想气体,温度升高时压强增大. 从分子动理论的角度分析,这是由于
分子热运动的 _________增大了. 该气体在温度T1、T2时的分子速率分布图象如下图所示,则T1 _________(选填“大于”或“小于”)T2.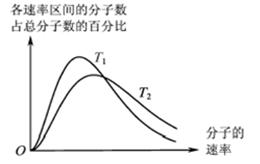
(3)如下图所示,一定质量的理想气体从状态A 经等压过程到状态B. 此过程中,气
体压强p =1.0*105 Pa,吸收的热量Q =7.0*102J,求此过程中气体内能的增量.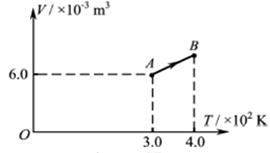
试题篮
()