高中物理综合题

受中子轰击时会发生裂变，产生和，同时放出能量.已知每个铀核裂变释放的平均能量为200 MeV.
(1)写出核反应方程;
(2)现在要建设发电功率为5×10⁵ kW的核电站，用²³⁵U作核燃料，假设核裂变释放的能量一半转化为电能，那么该核电站一天消耗²³⁵U多少千克？(阿伏加德罗常数取6.0×10²³ mol^-1)

原子反应堆的功率为10⁴ kW,1 h消耗的燃料为8.75 g.已知每个²³⁵U裂变时放出的核能为2×10⁸ eV，求核燃料中²³⁵U所占的百分比.

科学家发现，太空中γ射线一般都是从很远的星体放射出来的.当γ射线爆发时，在数秒钟内所产生的能量，相当于太阳在过去一百亿年所发出的能量总和的一千倍左右，大致上等于太阳全部静质量所对应的能量的总和.科学家利用超级计算机对γ射线爆发的状态进行了模拟.经过模拟，发现γ射线爆发是起源于一个垂死的星球的“坍塌”过程，只有星球“坍塌”时，才可以发出这么巨大的能量.已知太阳光照射到地球上大约需要8 min.由此来估算：在宇宙中，一次γ射线爆发所放出的能量.(G=6.67×10^-11 N·m²/kg²，结果保留两位有效数字)

²³⁸U的半衰期是4.5×10⁹年，假设一块矿石中含有2 kg的²³⁸U.求：
(1)经过45亿年后，还剩多少²³⁸U?
(2)假设发生衰变的铀都变成了²⁰⁶Pb，矿石中含有多少铅？
(3)这时铀、铅的质量之比是多少？

中子、质子、氘核D的质量分别为m_n、m_p、m_D.现用光子能量为E的γ射线照射静止氘核，使之分解.用核符号写出上述核反应方程，若分解后的中子、质子的动能相等，则中子的动能是多少？

密度为ρ=0．5×10³kg／m³的小木球，从离水面高h=5m处由静止开始自由下落，然后落入足够深的水池中，如图5-3-19所示，若不计空气阻力和水的黏滞阻力，球在与水面撞击时无机械能损失．求：小木球在水中能下沉多深?

如图5-3-18所示，三个物体质量分别为m₁、m₂、m₃，带有滑轮的物体放在光滑水平面上，滑轮和所有接触处的摩擦及绳的质量均不计，要使三个物体无相对运动，则水平推力F为多少?

已知如图，E =6V，r =4Ω，R1=2Ω，R2的变化范围是0~10Ω。求：
①电源的最大输出功率；
②R1上消耗的最大功率；
③R2上消耗的最大功率。

长L=60cm质量为m=6.0×10-2kg，粗细均匀的金属棒，两端用完全相同的弹簧挂起，放在磁感强度为B=0.4T，方向垂直纸面向里的匀强磁场中，如图8所示，若不计弹簧重力，问(1)要使弹簧不伸长，金属棒中电流的大小和方向如何?(2)如在金属中通入自左向右、大小为I=0.2A的电流，金属棒下降=1cm，若通入金属棒中的电流仍为0.2A，但方向相反，这时金属棒下降了多少?

如图所示，两平行光滑导轨相距为L=20cm，金属棒MN的质量为m=10g，电阻R=8Ω，匀强磁场磁感应强度B方向竖直向下，大小为B=0.8T，电源电动势为E=10V，内阻r=1Ω。当电键S闭合时，MN处于平衡，求变阻器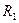的取值为多少?(设θ=45°)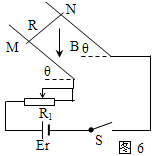

如图22所示，两个共轴的圆筒形金属电极，外电极接地，其上均匀分布着平行于轴线的四条狭缝ａ、ｂ、ｃ和ｄ，外筒的外半径为ｒ，在圆筒之外的足够大区域中有平行于轴线方向的均匀磁场，磁感强度的大小为Ｂ。在两极间加上电压，使两圆筒之间的区域内有沿半径向外的电场。一质量为ｍ、带电量为＋ｑ的粒子，从紧靠内筒且正对狭缝ａ的Ｓ点出发，初速为零。如果该粒子经过一段时间的运动之后恰好又回到出发点Ｓ，则两电极之间的电压Ｕ应是多少？（不计重力，整个装置在真空中）

核聚变反应需要几百万度以上的高温，为把高温条件下高速运动的离子约束在小范围内（否则不可能发生核反应），通常采用磁约束的方法（托卡马克装置）。如图所示，环状匀强磁场围成中空区域，中空区域中的带电粒子只要速度不是很大，都不会穿出磁场的外边缘而被约束在该区域内。设环状磁场的内半径为R1=0.5m，外半径R2=1.0m，磁场的磁感强度B=1.0T，若被束缚带电粒子的荷质比为q/m=4×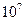c/㎏，中空区域内带电粒子具有各个方向的速度。试计算

（1）粒子沿环状的半径方向射入磁场，不能穿越磁场的最大速度。
（2）所有粒子不能穿越磁场的最大速度。

如图7所示，在的区域内存在匀强磁场，磁场方向垂直于xOy平面并指向纸面外，磁感应强度为B。一带正电的粒子以速度从O点射入磁场，入射方向在xy平面内，与x轴正方向的夹角为。若粒子射出磁场的位置与O点的距离为L，求该粒子的电量和质量之比q/m。

如图所示电路，已知电源电动势ε=6.3V，内电阻r=0.5Ω，固定电阻R1=2Ω，R2=3Ω，R3是阻值为5Ω的滑动变阻器。按下电键K，调节滑动变阻器的触点，求通过电源的电流范围。

如图所示，电源电压保持不变，在滑片P自右向左滑动过程中，的电功率如何变化？