高中物理综合题

建筑工地上的黄沙堆成圆锥形，而且不管如何堆其角度是不变的。若测出其圆锥底的周长为12．5m，高为1．5m，如图所示。
试求黄沙之间的动摩擦因数。
若将该黄沙靠墙堆放，占用的场地面积至少为多少？

如图10是为了检验某种防护罩承受冲击能力的装置，M为半径为、固定于竖直平面内的光滑圆弧轨道，轨道上端切线水平，N为待检验的固定曲面，该曲面在竖直面内的截面为半径的圆弧，圆弧下端切线水平且圆心恰好位于M轨道的上端点，M的下端相切处置放竖直向上的弹簧枪，可发射速度不同的质量的小钢珠，假设某次发射的钢珠沿轨道恰好能经过M的上端点，水平飞出后落到N的某一点上，取，求：
发射该钢珠前，弹簧的弹性势能多大？
钢珠落到圆弧上时的速度大小是多少？（结果保留两位有效数字）

如图所示，PR是一块长为L="4" m的绝缘平板固定在水平地面上，整个空间有一个平行于PR的匀强电场E，在板的右半部分有一个垂直于纸面向外的匀强磁场B，一个质量为m=0．1 kg，带电量为q=0．5 C的物体，从板的P端由静止开始在电场力和摩擦力的作用下向右做匀加速运动，进入磁场后恰能做匀速运动。当物体碰到板R端的挡板后被弹回，若在碰撞瞬间撤去电场，物体返回时在磁场中仍做匀速运动，离开磁场后做匀减速运动停在C点，PC=L/4，物体与平板间的动摩擦因数为μ=0．4，取g=10m/s² ，求：

判断物体带电性质，正电荷还是负电荷？
物体与挡板碰撞前后的速度v₁和v₂
磁感应强度B的大小
电场强度E的大小和方向

开普勒三定律也适用于神舟七号飞船的变轨运动. 飞船与火箭分离后进入预定轨道, 飞船在近地点(可认为近地面)开动发动机加速, 之后，飞船速度增大并转移到与地球表面相切的椭圆轨道, 飞船在远地点再次点火加速, 飞船沿半径为r的圆轨道绕地运动. 设地球半径为R，地球表面的重力加速度为g，若不计空气阻力，试求神舟七号从近地点到远地点时间（变轨时间）.

神奇的黑洞是近代引力理论所预言的一种特殊天体，探寻黑洞的方案之一是观测双星系统的运动规律．天文学家观测河外星系大麦哲伦云时，发现了LMCX-3双星系统，它由可见星A和不可见的暗星B构成．两星视为质点，不考虑其它星体的影响，A、B围绕两者连线上的O点做匀速圆周运动，它们之间的距离保持不变，如图18所示．引力常量为G，由观测能够得到可见星A的速率v和运行周期T．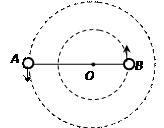

可见星A所受暗星B的引力F_A可等效为位于O点处质量为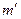的星体（可视为质点）对它的引力，设A和B的质量分别为m₁、m₂，试求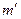（用m₁、m₂表示）；
求暗星B的的质量m₂与可见星A的速率v、运行周期T和质量m₁之间的关系式；
恒星演化到末期，如果其质量大于太阳质量m_s的2倍，它将有可能成为黑洞．若可见星A的速率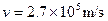，运行周期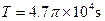，质量m₁=6m_s，试通过估算来判断暗星B有可能是黑洞吗？  图18
（，）

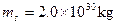    如图所示，两倾角分别为37°和53°的两个斜面体放置在水平面上，顶点对接于O点，并将它们固定，将一小球自斜面上的A点以大小为v₀的速度水平抛出，恰好垂直打在斜面2上，已知A点到到O点的距离为L=1m，g取10m/s², 求v₀大小。

已知地球表面积为S，空气的平均摩尔质量为M，阿伏加德罗常数为NA，大气压强为p0，写出地球周围大气层的空气分子数的表达式.若S=5.1×1014 m2，M=2.9×10-2 kg/mol，NA=6.0×1023 mol-1，p0=1.0×105 Pa，则地球周围大气层的空气分子数约为多少个？（取两位有效数字）

如图所示,匀强磁场的磁感应强度B="0.5" T,边长L="10" cm的正方形线圈abcd共100匝,线圈电阻r="1" Ω,线圈绕垂直于磁感线的对称轴OO′匀速转动,角速度ω=2π rad/s,外电路电阻R="4" Ω.求：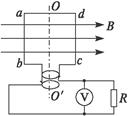

(1)转动过程中感应电动势的最大值;
(2)由图示位置(线圈平面与磁感线平行)转过60°角时的瞬时感应电动势;
(3)由图示位置转过60°角的过程中产生的平均感应电动势;
(4)交流电压表的示数;
(5)转动一周外力做的功.

如图所示，abc为固定在水平面上的光滑圆弧轨道，b点为最低点，O为圆心，弧abc所对圆心角小于5°，现将甲球由O点、乙球由a点同时由静止释放（把两球视为质点），若不计空气阻力，哪个球先到达b点？

如图所示，带正电小球质量为m=1×10-2 kg，带电荷量为q=1×10-6 C,置于光滑绝缘水平面上的A点.当空间存在着斜向上的匀强电场时，该小球从静止开始始终沿水平面做匀加速直线运动，当运动到B点时，测得其速度vb="1.5" m/s，此时小球的位移为s="0.15" m.求此匀强电场场强E的取值范围.（g取10 m/s2）

某同学求解如下：设电场方向与水平面之间夹角为θ,由动能定理qEscosθ=mvB2-0,得E== V/m，由题意可知θ＞0,所以当E＞7.5×104 V/m时小球将始终沿水平面做匀加速直线运动.
经检查，计算无误.该同学所得结论是否有不完善之处？若有请予以补充.

如下图所示，在绝缘水平面上，相距为L的A、B两点处分别固定着两个等量正电荷，a、b是AB连线上两点，其中Aa=Bb=,O为AB连线中点.一质量为m、电荷量为+q的小滑块（可视为质点）以初动能Ek0从a点出发，沿AB直线向b点运动，其中小滑块第一次经过O点时的动能为初动能的n倍（n＞1）,到达b点时动能恰好为零，小滑块最终停在O点.求：

（1）小滑块与水平面间的滑动摩擦因数μ；
（2）O、b两点间的电势差UOb；
（3）小滑块运动的总路程s.

如图所示，A、B、C表示匀强电场中的三点，它们的电势分别为φA="-5" V,φB="9" V,φC="2" V.试在图中画出过A、B、C点的三条等势线，并画出一条过C点的电场线.

三只电阻R1“30 Ω30 W”,R2“10 Ω40 W”，R3“3 Ω27 W”？将它们串联时，消耗的总功率不应超过多少？将它们并联时，消耗的总功率不能超过多少？

如图11-2-15所示，在倾角为30⁰的斜面上，放置两条宽L=0.5m的平行导轨，将电源、滑动变阻器用导线连接在导轨上，在导轨上横放一根质量m=0.2kg的金属杆ab，电源电动势E=12V，内阻r=0．3Ω，金属杆与导轨间最大静摩擦力为fm=0.6N，磁场方向垂直轨道所在平面，B=0.8T．金属杆ab的电阻为0.2Ω，导轨电阻不计．欲使杆的轨道上保持静止，滑动变阻器的使用电阻的范围多大?(g取10m／s²)

两极板M、N相距为d，板长为3d，两极板都未带电，板间有垂直于纸面向外的匀强磁场，如图11-3-18所示，一群电子沿平行于极板的方向从各个位置以速度V射入板间．为了使电子都不从板间穿出，磁感应强度B的取值范围是怎样的?(设电子电量为e、质量为m)