整除1.173□是一个四位数.数学老师说:“我在其中的方框内中先后填入3个数字,所得到的3个四位数:依次可被9,1l,6整除.”问:数学老师先后填入的3个数字的和是多少?
有一串数:1,1,2,3,5,8,……,从第三个数起,每个数都是前两个数之和,在这串数的前2009个数中,有几个是5的倍数?
一个大于10的自然数去除90、164后所得的两个余数的和等于这个自然数去除220后所得的余数,则这个自然数是多少?
3个三位数乘积的算式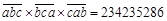 (其中
(其中 ), 在校对时,发现右边的积的数字顺序出现错误,但是知道最后一位6是正确的,问原式中的
), 在校对时,发现右边的积的数字顺序出现错误,但是知道最后一位6是正确的,问原式中的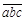 是多少?
是多少?
已知自然数A、B满足以下2个性质:(1)A、B不互质 (2)A、B的最大公约数与最小公倍数之和为35。那么A+B的最小值是多少?
设A共有9个不同的约数,B共有6个不同的约数,C共有8个不同的约数,这三个数中的任何两个都不整除,则这三个数之积的最小值是多少?
试题篮
()