在平面直角坐标系中,点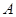 和点
和点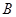 关于原点对称,已知点
关于原点对称,已知点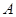 的坐标为(
的坐标为(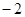 ,
,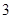 ),那么点
),那么点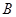 的坐标为( )
的坐标为( )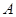 .(
.(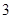 ,
,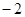 );
); 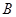 .(
.(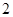 ,
,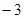 );
);  .(
.(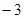 ,
,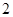 );
); 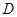 .(
.(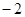 ,
,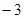 ).
).
打开某洗衣机开关,在(洗衣机内无水)洗涤衣服时,洗衣机经历了进水、清洗、排水、脱水四个连续过程,其中进水、清洗、排水时洗衣机中的水量y(升)与时间x(分钟)之间满足某种函数关系,其函数图象大致为( )
无论实数m取什么值,直线y=x+ m与y=-x+5的交点都不能在( )
m与y=-x+5的交点都不能在( )
| A.第一象限 | B.第二象限 | C.第三象限 | D.第四象限 |
点A的坐标 满足条件
满足条件 ,则点A的位置在: ( )
,则点A的位置在: ( )
| A.第一象限 | B.第二象限 | C.第三象限 | D.第四象限 |
如图,在平面直角坐标系中,四边形OABC是菱形,点C的坐标为(4,0)∠AOC= 60°,垂直于x轴的直线l从y轴出发,沿x轴正方向以每秒1个单位长度的速度向右平移,设直线l与菱形OABC的两边分别交于点M,N(点M在点N的上方),若△OMN的面积为S,直线l的运动时间为t 秒(0≤t≤4),则能大致反映S与t的函数关系的图象是( ) 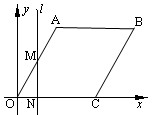
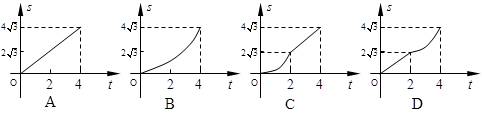
如图,下列各种情境分别可以用那幅图来近似地刻画一杯越来越凉的水(水温与时间的关系)
下列说法中正确的是( )
A.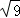 是一个无理数 是一个无理数 |
B.函数y=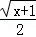 的自变量的取值范围是x>﹣1 的自变量的取值范围是x>﹣1 |
C.若点P(2,a)和点Q(b,﹣3)关于x轴对称,则a﹣b的值为1 |
D.﹣8的立方根是2 |
已知点P(a,a+2)在直线y=2x—l上,则点P关于原点的对称点P’的坐标可表示为
| A.(3,5) | B.(一3,5) |
| C.(3,一5) | D.(一3,一5) |
已知两个变量x和y,它们之间的3组对应值如下表所示.
| x |
-1 |
0 |
1 |
| y |
-1 |
1 |
3 |
则y 与x之间的函数关系式可能是【 】
A.y=x B.y=2x+1 C.y=x2+x+1 D.y=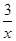
如图,直线 ,点
,点 坐标为(1,0),过点
坐标为(1,0),过点 作
作 轴的垂线交直线于点
轴的垂线交直线于点 B,以原点O为圆心,
B,以原点O为圆心, 长为半径画弧交
长为半径画弧交 轴于点
轴于点 ;再过点
;再过点 作
作 的垂线交直线于点
的垂线交直线于点 ,以原点O为圆心,
,以原点O为圆心, 长为半径画弧交
长为半径画弧交 轴于点
轴于点 ,…,按此做法进行下去,点
,…,按此做法进行下去,点 的坐标为( ).
的坐标为( ).
A. |
B. |
C. |
D. |

已知抛物线 的图象如图所示,则下列结论:①
的图象如图所示,则下列结论:① >0;
>0;
② ; ③
; ③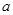 <
< ; ④
; ④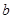 >1.其中正确的结论是 ( )
>1.其中正确的结论是 ( )
| A.①② | B.②③ | C.③④ | D.②④ |
小明从家骑车上学,先上坡到达A地后再下坡到达学校,所用的时间与路程如图所示.如果返回时,上、下坡的速度仍然保持不变,那么他从学校回到家需要的时间是( )
| A.8.6分钟 | B.9分钟 | C.12分钟 | D.16分钟 |

如图,直角梯形AOCD的边OC在x轴上,O为坐标原点,CD垂直于x轴,D(5,4),AD=2.若动点E、F同时从点O出发,E点沿折线OA→AD→DC运动,到达C点时停止;F点沿OC运动,到达C点是停止,它们运动的速度都是每秒1个单位长度.设E运动秒x时,△EOF的面积为y(平方单位),则y关于x的函数图象大致为( )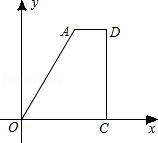

试题篮
()