在平面直角坐标系中,点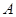 和点
和点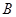 关于原点对称,已知点
关于原点对称,已知点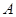 的坐标为(
的坐标为(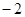 ,
,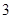 ),那么点
),那么点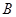 的坐标为( )
的坐标为( )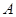 .(
.(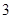 ,
,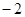 );
); 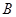 .(
.(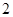 ,
,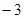 );
);  .(
.(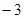 ,
,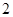 );
); 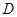 .(
.(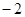 ,
,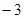 ).
).
如图,在平面直角坐标系中,函数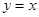 的图象
的图象 是第一、三象限的角平分线.
是第一、三象限的角平分线.
实验与探究:由图观察易知A(0,2)关于直线 的对称点
的对称点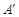 的坐标为(2,0),请在图中分别标明B(5,3) 、C(-2,5) 关于直线
的坐标为(2,0),请在图中分别标明B(5,3) 、C(-2,5) 关于直线 的对称点
的对称点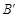 、
、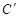 的位置,并写出它们的坐标:
的位置,并写出它们的坐标: 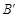 、
、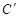 ;
;
归纳与发现:结合图形观察以上三组点的坐标,你会发现:坐标平面内任一点P(m,n)关于第一、三象限的角平分线 的对称点
的对称点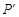 的坐标为 ;
的坐标为 ;
运用与拓广:已知两点D(0,-3)、E(-1,-4),试在直线 上确定一点Q,使点Q到D、E两点的距离之和最小,并求出Q点坐标.
上确定一点Q,使点Q到D、E两点的距离之和最小,并求出Q点坐标.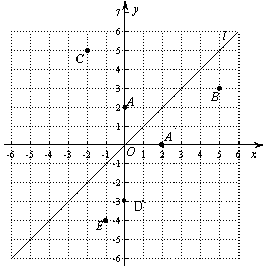
如图,下列各种情境分别可以用那幅图来近似地刻画一杯越来越凉的水(水温与时间的关系)
下列说法中正确的是( )
A.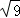 是一个无理数 是一个无理数 |
B.函数y=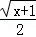 的自变量的取值范围是x>﹣1 的自变量的取值范围是x>﹣1 |
C.若点P(2,a)和点Q(b,﹣3)关于x轴对称,则a﹣b的值为1 |
D.﹣8的立方根是2 |
已知点P(a,a+2)在直线y=2x—l上,则点P关于原点的对称点P’的坐标可表示为
| A.(3,5) | B.(一3,5) |
| C.(3,一5) | D.(一3,一5) |
已知两个变量x和y,它们之间的3组对应值如下表所示.
| x |
-1 |
0 |
1 |
| y |
-1 |
1 |
3 |
则y 与x之间的函数关系式可能是【 】
A.y=x B.y=2x+1 C.y=x2+x+1 D.y=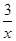
在函数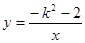 (
( 为常数)的图象上有三个点(-2,
为常数)的图象上有三个点(-2, ),(-1,
),(-1, ),(
),(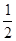 ,
, ),函数值
),函数值 ,
, ,
, 的大小为 .
的大小为 .
下面的图标列出了一项试验的统计数据,表示将皮球从高处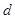 落下时,弹跳高度
落下时,弹跳高度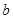 与下落高度
与下落高度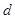 的关系:下面式子中能表示这种关系的是( )
的关系:下面式子中能表示这种关系的是( )
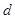 |
50 |
80 |
100 |
150 |
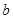 |
25 |
40 |
50 |
75 |
A.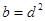 B.
B.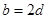
C.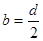 D.
D.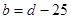
如图,在半径为5的⊙O中,弦AB=6,点C是优弧 上一点(不与A,B重合),则cosC的值为 .
上一点(不与A,B重合),则cosC的值为 .
如图2,在Rt△ABC中,OA=2,AB=1,把Rt△ABO绕着原点逆时针旋转90°,得△A'B'O,那么点A'的坐标为 ( )
A.( ,1) ,1) |
B.(1, ) ) |
C.( , , ) ) |
D.( , , ) ) |

试题篮
()