初中数学幂的乘方与积的乘方试题

有以下两下数串：1，3，5，7，…1991，1993，1995，1997，1999和1，4，7，10…1990，1993，1996，1999，同时出现在这两个数串中的数的个数共有____________个．

在求1+6²+6³+6⁴+6⁵+6⁶+6⁷+6⁸+6⁹的值时，小林发现：从第二个加数起每一个加数都是前一个加数的6倍，于是她设：
S=1+6²+6³+6⁴+6⁵+6⁶+6⁷+6⁸+6⁹①
然后在①式的两边都乘以6，得：
6S=6+6²+6³+6⁴+6⁵+6⁶+6⁷+6⁸+6⁹+6¹⁰②
②﹣①得6S﹣S=6¹⁰﹣1，即5S=6¹⁰﹣1，所以S=，得出答案后，爱动脑筋的小林想：
如果把“6”换成字母“a”（a≠0且a≠1），能否求出1+a+a²+a³+a⁴+…+a²⁰¹⁴的值？你的答案是（　　）

A．

B．

C．

D．a^2014﹣1

有一列数如下：1，0，1，0，0，1，0，0，0，1，0，0，0，0，1，…，则第9个1在这列数中是第　    　个数．

如图，A点的初始位置位于数轴上的原点，现对A点做如下移动：第1次从原点向右移动1个单位长度至B点，第2次从B点向左移动3个单位长度至C点，第3次从C点向右移动6个单位长度至D点，第4次从D点向左移动9个单位长度至E点，…，依此类推，这样至少移动 28 次后该点到原点的距离不小于41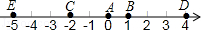

为了求1+2+2²+2³+…+2¹⁰⁰的值，可令S=1+2+2²+2³+…+2¹⁰⁰，则2S=2+2²+2³+2⁴+…+2¹⁰¹，因此2S﹣S=2¹⁰¹﹣1，所以S=2¹⁰¹﹣1，即1+2+2²+2³+…+2¹⁰⁰=2¹⁰¹﹣1，仿照以上推理计算1+3+3²+3³+…+3²⁰¹⁴的值是　   　．

一对小兔子从出生到第三个月就可以长大，并且生一对小兔子，以后每个月可以生一对小兔子，新生的小兔子三个月后又可以生小兔子．如果你也有一对刚出生的小兔子，那么到第10个月你所有的兔子的对数是（ ）

A．9

B．89

C．21

D．28

王老师在教学过程中善于把数学知识与实际生活联系在一起．在课堂上，他把全班同学分成五组，编号分别是A、B、C、D、E，每组的人数分别是10、7、9、8、6．游戏规则：当他数完1后，人数最少的那一组学生不动，其他各组各出一个人去人数最少的那组；当他数完2后，此时人数最少的那一组学生不动，其他各组再各出一个人去人数最少的那组…如此进行下去，那么当王老师数完2 008后，A、B、C、D、E五个组中的人数依次是（ ）
A．9、6、8、7、10
B．7、9、6、10、8
C．6、8、10、9、7
D．8、10、7、6、9

将正偶数按下表排成5列

	第1列	第2列	第3列	第4列	第5列
第1行		2	4	6	8
第2行	16	14	12	10
第3行		18	20	22	24
第4行	32	30	28	26
…		…

根据上面排列的规律，2012应排在（ ）
A．第502行第1列
B．第250行第5列
C．第251行第4列
D．第252行第3列

如图是中国古代著名的“杨辉三角形”的示意图．图中填入的所有数的总和等于（ ）

A．126

B．127

C．128

D．129

将1、2、3、4、5、6这六个数字分别填入每个小方格中，如果要求每行、每列及每个对角线隔成的2×3方格内部都没有重复数字，则“▲”处填入的数字是（ ）

A．5

B．4

C．3

D．2

四个小朋友站成一排，老师按图中所示的规则数数，数到2014时对应的小朋友可得一朵红花．那么，得红花的小朋友是（ ）

A．小沈

B．小叶

C．小李

D．小王

算：

一个正整数能表示为两个正整数的平方差，则称这个正整数为“智慧数”（如3=，16=）．已知智慧数按从小到大顺序构成如下数列：
3，5，7，8，9，11，12，13，15，16，17，19，20，21，23，24，25，…．
则第2006个智慧数是（　　）

A．2672

B．2675

C．2677

D．2680

如图是中国古代著名的“杨辉三角形”的示意图．图中填入的所有数的总和等于（　　）

A．126

B．127

C．128

D．129

（1）通过计算比较下列各式中两数的大小：（填“＞”、“＜”或“=”）
①1^-2   2^-1，②2^-3   3^-2，③3^-4    4^-3，④4^-5    5^-4，…
（2）由（1）可以猜测n^-（n+1）与（n+1）^-n（n为正整数）的大小关系：
当n        时，n^-（n+1）＞（n+1）^-n；当n    时，n^-（n+1）＜（n+1）^-n．