我们自从有了用字母表示数,发现表达有关的数和数量关系更加的简洁明了,从而更助于我们发现更多有趣的结论,请你按要求试一试:
(1)用代数式表示:
①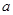 与
与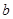 的平方的差;
的平方的差;
②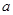 ,
,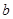 两数的和与
两数的和与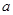 ,
,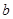 两数的差的乘积.
两数的差的乘积.
(2)当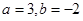 时,求第(1)题中①②所列的代数式的值,根据计算的结果你发现了什么等式?
时,求第(1)题中①②所列的代数式的值,根据计算的结果你发现了什么等式?
(3)利用(2)中发现的结论,用简便方法计算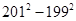 的值.
的值.
下列计算中,错误的有( )
①(3a+4)(3a-4)=9a2-4;
②(2a2-b)(2a2+b)=4a2-b2;
③(3-x)(x+3)=x2-9;
④(-x+y)·(x+y)=-(x-y)(x+y)=-x2-y2.
| A.1个 | B.2个 | C.3个 | D.4个 |
在下列多项式的乘法中,可以用平方差公式计算的是( )
| A.(x+1)(1+x) | B.( a+b)(b- a+b)(b- a) a) |
| C.(-a+b)(a-b) | D.(x2-y)(x+y2) |
下列运算中,正确的是( )
| A.(a+3)(a-3)=a2-3 | B.(3b+2)(3b-2)=3b2-4 |
| C.(3m-2n)(-2n-3m)=4n2-9m2 | D.(x+2)(x-3)=x2-6 |
试题篮
()