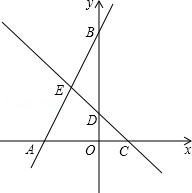
如图,在平面直角坐标系中,点O为坐标原点,直线 与坐标轴交于C,D两点,直线AB与坐标轴交于A,B两点,线段OA,OC的长是方程 的两个根 .
(1)求点A,C的坐标;
(2)直线AB与直线CD交于点E,若点E是线段AB的中点,反比例函数 的图象的一个分支经过点E,求k的值;
(3)在(2)的条件下,点M在直线CD上,坐标平面内是否存在点N,使以点B,E,M,N为顶点的四边形是菱形?若存在,请直接写出满足条件的点N的坐标;若不存在,请说明理由.
一个菱形的边长是方程 x 2﹣8 x+15=0的一个根,其中一条对角线长为8,则该菱形的面积为( )
| A. |
48 |
B. |
24 |
C. |
24或40 |
D. |
48或80 |
(1)化简求值: ,其中 x是一元二次方程 x( x﹣1)=2 x﹣2的解.
(2)解不等式组: ,并求其整数解的和.
关于的一元二次方程
有实数根.
(1)求的取值范围;
(2)如果是符合条件的最大整数,且一元二次方程
与方程
有一个相同的根,求此时
的值.
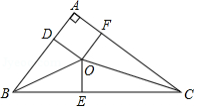
我国古代数学家刘徽将勾股形(古人称直角三角形为勾股形)分割成一个正方形和两对全等的三角形,如图所示,已知 , , ,则正方形 的边长是
| A. |
|
B. |
2 |
C. |
|
D. |
4 |
试题篮
()