初中数学一次函数的应用填空题

甲、乙两人沿同一条直路走步，如果两人分别从这条直路上的 $A$， $B$两处同时出发，都以不变的速度相向而行，图1是甲离开 $A$处后行走的路程 $y$（单位： $m)$与行走时间 $x$（单位： $\mathit{min})$的函数图象，图2是甲、乙两人之间的距离 $y$（单位： $m)$与甲行走时间 $x$（单位： $\mathit{min})$的函数图象，则 $a-b=$　　．

甲、乙两人分别从 $A$， $B$两地相向而行，他们距 $B$地的距离 $s\left(\mathit{km}\right)$与时间 $t\left(ℎ\right)$的关系如图所示，那么乙的速度是　　 $\mathit{km}/ℎ$．

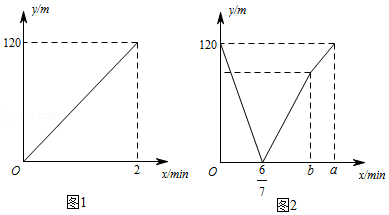
一辆快车从甲地开往乙地，一辆慢车从乙地开往甲地，两车同时出发，设快车离乙地的距离为 $y_1\left(\mathit{km}\right)$，慢车离乙地的距离为 $y_2\left(\mathit{km}\right)$，慢车行驶时间为 $x\left(h\right)$，两车之间的距离为 $s\left(\mathit{km}\right)$． $y_1$， $y_2$与 $x$的函数关系图象如图1所示， $s$与 $x$的函数关系图象如图2所示．则下列判断：①图1中 $a=3$；②当 $x=\frac{15}{8}h$时，两车相遇；③当 $x=\frac{3}{2}$时，两车相距 $60\mathit{km}$；④图2中 $C$点坐标为 $(3,180)$；⑤当 $x=\frac{5}{8}h$或 $\frac{25}{8}h$时，两车相距 $200\mathit{km}$．其中正确的有　　（请写出所有正确判断的序号）

如图，小明购买一种笔记本所付款金额 $y$（元 $)$与购买量 $x$（本 $)$之间的函数图象由线段 $\mathit{OB}$和射线 $\mathit{BE}$组成，则一次购买8个笔记本比分8次购买每次购买1个可节省　　元．

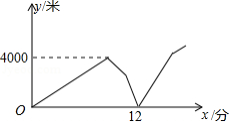
如图，在平面直角坐标系xOy中，▱ABCO的顶点A，B的坐标分别是A（3，0），B（0，2）．动点P在直线 $y=\frac{3}{2}x$上运动，以点P为圆心，PB长为半径的⊙P随点P运动，当⊙P与▱ABCO的边相切时，P点的坐标为　　．

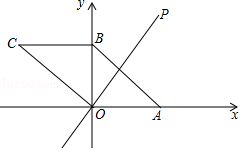
如图，将八个边长为1的小正方形摆放在平面直角坐标系中，若过原点的直线 l将图形分成面积相等的两部分，则将直线 l向右平移3个单位后所得直线 l′的函数关系式为 　 　．

甲、乙两人沿笔直公路匀速由 $A$ 地到 $B$ 地，甲先出发30分钟，到达 $B$ 地后原路原速返回与乙在 $C$ 地相遇．甲的速度比乙的速度快 $35\mathit{km}/h$ ，甲、乙两人与 $A$ 地的距离 $y\left(\mathit{km}\right)$ 和乙行驶的时间 $x\left(h\right)$ 之间的函数关系如图所示，则 $B$ ， $C$ 两地的距离为 　 　 $\mathit{km}$ （结果精确到 $1\mathit{km})$ ．

某公司新产品上市30天全部售完，图1表示产品的市场日销售量与上市时间之间的关系，图2表示单件产品的销售利润与上市时间之间的关系，则最大日销售利润是　　元．

某市为提倡居民节约用水，自今年1月1日起调整居民用水价格．图中、分别表示去年、今年水费（元与用水量之间的关系．小雨家去年用水量为，若今年用水量与去年相同，水费将比去年多　　元．

元朝朱世杰的《算学启蒙》一书记载：“今有良马日行二百四十里，驽马日行一百五十里．驽马先行一十二日，问良马几何日追及之．”如图是两匹马行走路程关于行走时间的函数图象，则两图象交点的坐标是　　．

一天，小明从家出发匀速步行去学校上学．几分钟后，在家休假的爸爸发现小明忘带数学书，于是爸爸立即匀速跑步去追小明，爸爸追上小明后以原速原路跑回家．小明拿到书后以原速的快步赶往学校，并在从家出发后23分钟到校（小明被爸爸追上时交流时间忽略不计）．两人之间相距的路程（米与小明从家出发到学校的步行时间（分钟）之间的函数关系如图所示，则小明家到学校的路程为　　米．

某公司快递员甲匀速骑车前往某小区送物件，出发几分钟后，快递员乙发现甲的手机落在公司，无法联系，于是乙匀速骑车去追赶甲．乙刚出发2分钟时，甲也发现自己手机落在公司，立刻按原路原速骑车回公司，2分钟后甲遇到乙，乙把手机给甲后立即原路原速返回公司，甲继续原路原速赶往某小区送物件，甲乙两人相距的路程（米与甲出发的时间（分钟）之间的关系如图所示（乙给甲手机的时间忽略不计）．则乙回到公司时，甲距公司的路程是　　米．

一天早晨，小玲从家出发匀速步行到学校，小玲出发一段时间后，她的妈妈发现小玲忘带了一件必需的学习用品，于是立即下楼骑自行车，沿小玲行进的路线，匀速去追小玲，妈妈追上小玲将学习用品交给小玲后，立即沿原路线匀速返回家里，但由于路上行人渐多，妈妈返回时骑车的速度只是原来速度的一半，小玲继续以原速度步行前往学校，妈妈与小玲之间的距离（米与小玲从家出发后步行的时间（分之间的关系如图所示（小玲和妈妈上、下楼以及妈妈交学习用品给小玲耽搁的时间忽略不计）．当妈妈刚回到家时，小玲离学校的距离为　　米．

，两地相距的路程为240千米，甲、乙两车沿同一线路从地出发到地，分别以一定的速度匀速行驶．甲车先出发40分钟后，乙车才出发．途中乙车发生故障，修车耗时20分钟，随后，乙车车速比发生故障前减少了10千米小时（仍保持匀速前行），甲、乙两车同时到达地．甲、乙两车相距的路程（千米）与甲车行驶时间（小时）之间的关系如图所示，求乙车修好时，甲车距地还有　　千米．

、两地之间的路程为2380米，甲、乙两人分别从、两地出发，相向而行，已知甲先出发5分钟后，乙才出发，他们两人在、之间的地相遇，相遇后，甲立即返回地，乙继续向地前行．甲到达地时停止行走，乙到达地时也停止行走．在整个行走过程中，甲、乙两人均保持各自的速度匀速行走，甲、乙两人相距的路程（米与甲出发的时间（分钟）之间的关系如图所示，则乙到达地时，甲与地相距的路程是　　米．