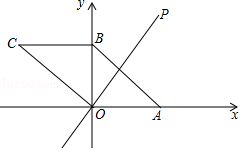
如图,在平面直角坐标系xOy中,▱ABCO的顶点A,B的坐标分别是A(3,0),B(0,2).动点P在直线 上运动,以点P为圆心,PB长为半径的⊙P随点P运动,当⊙P与▱ABCO的边相切时,P点的坐标为 .
甲、乙两动点分别从线段 的两端点同时出发,甲从点 出发,向终点 运动,乙从点 出发,向终点 运动.已知线段 长为 ,甲的速度为 .设运动时间为 ,甲、乙两点之间的距离为 , 与 的函数图象如图所示,则图中线段 所表示的函数关系式为 .(并写出自变量取值范围)

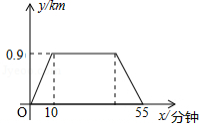
甲、乙两人沿笔直公路匀速由 地到 地,甲先出发30分钟,到达 地后原路原速返回与乙在 地相遇.甲的速度比乙的速度快 ,甲、乙两人与 地的距离 和乙行驶的时间 之间的函数关系如图所示,则 , 两地的距离为 (结果精确到 .

, 两地相距 ,甲货车从 地以 的速度匀速前往 地,到达 地后停止.在甲出发的同时,乙货车从 地沿同一公路匀速前往 地,到达 地后停止.两车之间的路程 与甲货车出发时间 之间的函数关系如图中的折线 所示.其中点 的坐标是 ,点 的坐标是 ,则点 的坐标是 .

某市为提倡居民节约用水,自今年1月1日起调整居民用水价格.图中 、 分别表示去年、今年水费 (元 与用水量 之间的关系.小雨家去年用水量为 ,若今年用水量与去年相同,水费将比去年多 元.

在一条笔直的公路上有 , , 三地, 地位于 , 两地之间,甲,乙两车分别从 , 两地出发,沿这条公路匀速行驶至 地停止.从甲车出发至甲车到达 地的过程,甲、乙两车各自与 地的距离 与甲车行驶时间 之间的函数关系如图表示,当甲车出发 时,两车相距 .

一天,小明从家出发匀速步行去学校上学.几分钟后,在家休假的爸爸发现小明忘带数学书,于是爸爸立即匀速跑步去追小明,爸爸追上小明后以原速原路跑回家.小明拿到书后以原速的 快步赶往学校,并在从家出发后23分钟到校(小明被爸爸追上时交流时间忽略不计).两人之间相距的路程 (米 与小明从家出发到学校的步行时间 (分钟)之间的函数关系如图所示,则小明家到学校的路程为 米.

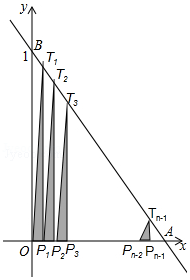
如图,直线 与两坐标轴分别交于 , 两点,将线段 分成 等份,分点分别为 , , , , ,过每个分点作 轴的垂线分别交直线 于点 , , , , ,用 , , , , 分别表示 △ , △ , , △ 的面积,则 .
一天早晨,小玲从家出发匀速步行到学校,小玲出发一段时间后,她的妈妈发现小玲忘带了一件必需的学习用品,于是立即下楼骑自行车,沿小玲行进的路线,匀速去追小玲,妈妈追上小玲将学习用品交给小玲后,立即沿原路线匀速返回家里,但由于路上行人渐多,妈妈返回时骑车的速度只是原来速度的一半,小玲继续以原速度步行前往学校,妈妈与小玲之间的距离 (米 与小玲从家出发后步行的时间 (分 之间的关系如图所示(小玲和妈妈上、下楼以及妈妈交学习用品给小玲耽搁的时间忽略不计).当妈妈刚回到家时,小玲离学校的距离为 米.

如图,已知菱形 的边 在 轴上,点 的坐标为 ,点 是对角线 上的一个动点,点 在 轴上,当 最短时,点 的坐标为 .

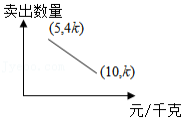
某人购进一批苹果到集贸市场零售,已知卖出的苹果数量与售价之间的关系如图所示,成本5元 千克,现以8元卖出,挣得 元.
小明从家步行到学校需走的路程为1800米.图中的折线 反映了小明从家步行到学校所走的路程 (米 与时间 (分钟)的函数关系,根据图象提供的信息,当小明从家出发去学校步行15分钟时,到学校还需步行 米.

小明从家到图书馆看报然后返回,他离家的距离 与离家的时间 之间的对应关系如图所示,如果小明在图书馆看报30分钟,那么他离家50分钟时离家的距离为 .
甲、乙两人分别从 , 两地相向而行,匀速行进甲先出发且先到达 地,他们之间的距离 与甲出发的时间 的关系如图所示,则乙由 地到 地用了 10 .

试题篮
()