已知二次函数 为常数),当自变量 的值满足 时,与其对应的函数值 的最大值为 ,则 的值为
A.3或6B.1或6C.1或3D.4或6
如图,若二次函数 图象的对称轴为 ,与 轴交于点 ,与 轴交于点 、点 ,则
①二次函数的最大值为 ;
② ;
③ ;
④当 时, .其中正确的个数是

A.1B.2C.3D.4
设 、 是任意两个实数,用 , 表示 、 两数中较大者,例如: , , , , , ,参照上面的材料,解答下列问题:
(1) , , , ;
(2)若 , ,求 的取值范围;
(3)求函数 与 的图象的交点坐标,函数 的图象如图所示,请你在图中作出函数 的图象,并根据图象直接写出 , 的最小值.

已知 a≥2, m 2﹣2 am+2=0, n 2﹣2 an+2=0, m≠ n,则( m﹣1) 2+( n﹣1) 2的最小值是( )
| A. |
6 |
B. |
3 |
C. |
﹣3 |
D. |
0 |
关于二次函数 ,下列说法错误的是
| A. |
若将图象向上平移10个单位,再向左平移2个单位后过点 ,则 |
| B. |
当 时, 有最小值 |
| C. |
对应的函数值比最小值大7 |
| D. |
当 时,图象与 轴有两个不同的交点 |
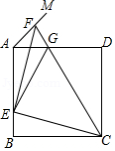
如图,正方形 的边长为 ,点 在边 上运动(不与点 , 重合), ,点 在射线 上,且 , 与 相交于点 ,连接 、 、 .则下列结论:
① ;
② 的周长为 ;
③ ;
④ 的面积的最大值是 ;
⑤当 时, 是线段 的中点.
其中正确的结论是
| A. |
①②③ |
B. |
②④⑤ |
C. |
①③④ |
D. |
①④⑤ |
如图,在正方形中,
,
为对角线
上一动点,连接
,
,过
点作
,交直线
于点
.
点从
点出发,沿着
方向以每秒
的速度运动,当点
与点
重合时,运动停止.设
的面积为
,
点的运动时间为
秒.

(1)求证:;
(2)求与
之间关系的函数表达式,并写出自变量
的取值范围;
(3)求面积的最大值.
试题篮
()