如图,利用一个直角墙角修建一个梯形储料场 ,其中 .若新建墙 与 总长为 ,则该梯形储料场 的最大面积是

A. B. C. D.
如图,在 中, , , .动点 从点 开始沿边 向点 以 的速度移动,动点 从点 开始沿边 向点 以 的速度移动.若 , 两点分别从 , 两点同时出发,在运动过程中, 的最大面积是

A. B. C. D.
一列自然数0,1,2,3, ,100.依次将该列数中的每一个数平方后除以100,得到一列新数.则下列结论正确的是
A.原数与对应新数的差不可能等于零
B.原数与对应新数的差,随着原数的增大而增大
C.当原数与对应新数的差等于21时,原数等于30
D.当原数取50时,原数与对应新数的差最大
如图所示,已知 中, , 边上的高 , 为 上一点, ,交 于点 ,交 于点 ,设点 到边 的距离为 .则 的面积 关于 的函数图象大致为

A. B.
B.
C. D.
D.
如图,在 中, , , ,点 从点 沿 向点 以 的速度运动,同时点 从点 沿 向点 以 的速度运动(点 运动到点 停止),在运动过程中,四边形 的面积最小值为

A. B. C. D.
足球运动员将足球沿与地面成一定角度的方向踢出,足球飞行的路线是一条抛物线,不考虑空气阻力,足球距离地面的高度 (单位: 与足球被踢出后经过的时间 (单位: 之间的关系如下表:
|
0 |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
|
|
0 |
8 |
14 |
18 |
20 |
20 |
18 |
14 |
|
下列结论:①足球距离地面的最大高度为 ;②足球飞行路线的对称轴是直线 ;③足球被踢出 时落地;④足球被踢出 时,距离地面的高度是 .其中正确结论的个数是
A.1B.2C.3D.4
如图,直线 的解析式为 ,它与 轴和 轴分别相交于 , 两点.平行于直线 的直线 从原点 出发,沿 轴的正方向以每秒1个单位长度的速度运动.它与 轴和 轴分别相交于 , 两点,运动时间为 秒 ,以 为斜边作等腰直角三角形 , 两点分别在 两侧).若 和 的重合部分的面积为 ,则 与 之间的函数关系的图象大致是

A. B.
B.
C. D.
D.
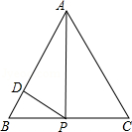
如图,正 的边长为4,点 为 边上的任意一点(不与点 、 重合),且 , 交 于点 .设 , ,则 关于 的函数图象大致是
A.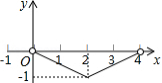
B.
C.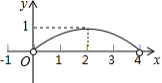
D.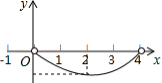
如图,在 中, , , ,点 在边 上,从点 向点 移动,点 在边 上,从点 向点 移动.若点 , 均以 的速度同时出发,且当一点移动到终点时,另一点也随之停止,连接 ,则线段 的最小值是

A. B. C. D.
如图,在 中, , , ,点 在 边上(不与点 重合),以 为对角线作平行四边形 ,连接 交 于点 .设 , ,则 与 之间的函数关系图象大致为

A. B.
B.
C. D.
D.
某校校园内有一个大正方形花坛,如图甲所示,它由四个边长为3米的小正方形组成,且每个小正方形的种植方案相同.其中的一个小正方形 如图乙所示, 米, 米,在五边形 区域上种植花卉,则大正方形花坛种植花卉的面积 与 的函数图象大致是

A. B.
B.
C. D.
D.
如图1,在矩形ABCD中,动点E从A出发,沿AB→BC方向运动,当点E到达点C时停止运动,过点E做FE⊥AE,交CD于F点,设点E运动路程为x,FC=y,如图2所表示的是y与x的函数关系的大致图象,当点E在BC上运动时,FC的最大长度是 ,则矩形ABCD的面积是( )
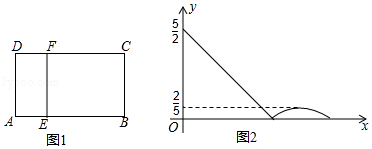
A. B.5C.6D.
如图,在平面直角坐标系中,已知 A(﹣3,﹣2), B(0,﹣2), C(﹣3,0), M是线段 AB上的一个动点,连接 CM,过点 M作 MN⊥ MC交 y轴于点 N,若点 M、 N在直线 y= kx+ b上,则 b的最大值是( )

| A. |
﹣ |
B. |
﹣ |
C. |
﹣1 |
D. |
0 |
如图,四边形 是边长为1的正方形,点 是射线 上的动点(点 不与点 ,点 重合),点 在线段 的延长线上,且 ,连接 ,将 绕点 顺时针旋转 得到 ,连接 , , .设 ,四边形 的面积为 ,下列图象能正确反映出 与 的函数关系的是

| A. |
|
B. |
|
| C. |
|
D. |
|
试题篮
()