初中数学等腰三角形的性质选择题

已知 $m$ 、 $n$ 、4分别是等腰三角形（非等边三角形）三边的长，且 $m$ 、 $n$ 是关于 $x$ 的一元二次方程 $x^2-6x+k+2=0$ 的两个根，则 $k$ 的值等于 $($ 　　 $)$

A．

7

B．

7或6

C．

6或 $-7$

D．

6

如图，在 $\mathit{\Delta ABC}$ 中， $\mathit{BA}=\mathit{BC}$ ， $\angle B=80°$ ，观察图中尺规作图的痕迹，则 $\angle \mathit{DCE}$ 的度数为 $($ 　　 $)$

A．

$60°$

B．

$65°$

C．

$70°$

D．

$75°$

如图， $\mathit{AB}$ 是 $\odot O$ 的弦， $\mathit{AC}$ 与 $\odot O$ 相切于点 $A$ ，连接 $\mathit{OA}$ ， $\mathit{OB}$ ，若 $\angle O=130°$ ，则 $\angle \mathit{BAC}$ 的度数是 $($ 　　 $)$

A．

$60°$

B．

$65°$

C．

$70°$

D．

$75°$

如图，在 $\mathit{\Delta ABC}$ 中， $\mathit{AB}=\mathit{AC}$ ．在 $\mathit{AB}$ 、 $\mathit{AC}$ 上分别截取 $\mathit{AP}$ ， $\mathit{AQ}$ ，使 $\mathit{AP}=\mathit{AQ}$ ．再分别以点 $P$ ， $Q$ 为圆心，以大于 $\frac{1}{2}\mathit{PQ}$ 的长为半径作弧，两弧在 $\angle \mathit{BAC}$ 内交于点 $R$ ，作射线 $\mathit{AR}$ ，交 $\mathit{BC}$ 于点 $D$ ．若 $\mathit{BC}=6$ ，则 $\mathit{BD}$ 的长为 $($ 　　 $)$

A．

2

B．

3

C．

4

D．

5

如图，点 $A$ ， $B$ ， $C$ 均在 $\odot O$ 上，当 $\angle \mathit{OBC}=40°$ 时， $\angle A$ 的度数是 $($ 　　 $)$

A．

$50°$

B．

$55°$

C．

$60°$

D．

$65°$

如图，矩形 $\mathit{ABCD}$ 的顶点 $A$ ， $B$ ， $C$ 分别落在 $\angle \mathit{MON}$ 的边 $\mathit{OM}$ ， $\mathit{ON}$ 上，若 $\mathit{OA}=\mathit{OC}$ ，要求只用无刻度的直尺作 $\angle \mathit{MON}$ 的平分线．小明的作法如下：连接 $\mathit{AC}$ ， $\mathit{BD}$ 交于点 $E$ ，作射线 $\mathit{OE}$ ，则射线 $\mathit{OE}$ 平分 $\angle \mathit{MON}$ ．有以下几条几何性质：①矩形的四个角都是直角，②矩形的对角线互相平分，③等腰三角形的"三线合一"．小明的作法依据是 $($ 　　 $)$

A．

①②

B．

①③

C．

②③

D．

①②③

如图， $\mathit{\Delta ABC}$ 中， $\mathit{AB}=\mathit{AC}=10$ ， $\tan A=2$ ， $\mathit{BE}\perp \mathit{AC}$ 于点 $E$ ， $D$ 是线段 $\mathit{BE}$ 上的一个动点，则 $\mathit{CD}+\frac{\sqrt{5}}{5}\mathit{BD}$ 的最小值是 $($ 　　 $)$

A．

$2\sqrt{5}$

B．

$4\sqrt{5}$

C．

$5\sqrt{3}$

D．

10

如图， $\mathit{PA}$ 、 $\mathit{PB}$ 为圆 $O$ 的切线，切点分别为 $A$ 、 $B$ ， $\mathit{PO}$ 交 $\mathit{AB}$ 于点 $C$ ， $\mathit{PO}$ 的延长线交圆 $O$ 于点 $D$ ，下列结论不一定成立的是 $($ 　　 $)$

A．

$\mathit{PA}=\mathit{PB}$

B．

$\angle \mathit{BPD}=\angle \mathit{APD}$

C．

$\mathit{AB}\perp \mathit{PD}$

D．

$\mathit{AB}$ 平分 $\mathit{PD}$

如图，在 $\text{Rt}\Delta \text{ABC}$ 中， $\angle \mathit{BAC}=90°$ ， $\angle B=36°$ ， $\mathit{AD}$ 是斜边 $\mathit{BC}$ 上的中线，将 $\mathit{\Delta ACD}$ 沿 $\mathit{AD}$ 对折，使点 $C$ 落在点 $F$ 处，线段 $\mathit{DF}$ 与 $\mathit{AB}$ 相交于点 $E$ ，则 $\angle \mathit{BED}$ 等于 $($ 　　 $)$

A．

$120°$

B．

$108°$

C．

$72°$

D．

$36°$

如图，将 $\odot O$ 沿弦 $\mathit{AB}$ 折叠， $\stackrel{̂}{\mathit{AB}}$ 恰好经过圆心 $O$ ，若 $\odot O$ 的半径为3，则劣 $\stackrel{̂}{\mathit{AB}}$ 的长为 $($ 　　 $)$

A．

$\frac{1}{2}\pi$

B．

$\pi$

C．

$2\pi$

D．

$3\pi$

如图， $\mathit{\Delta ABC}$ 是 $\odot O$ 的内接三角形， $\angle A=119°$ ，过点 $C$ 的圆的切线交 $\mathit{BO}$ 于点 $P$ ，则 $\angle P$ 的度数为 $($ 　　 $)$

A．

$32°$

B．

$31°$

C．

$29°$

D．

$61°$

如图， $\mathit{AB}$ 是 $\odot O$ 的直径， $C$ ， $D$ 是 $\odot O$ 上的两点，且 $\mathit{BC}$ 平分 $\angle \mathit{ABD}$ ， $\mathit{AD}$ 分别与 $\mathit{BC}$ ， $\mathit{OC}$ 相交于点 $E$ ， $F$ ，则下列结论不一定成立的是 $($ 　　 $)$

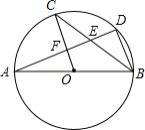
A．

$\mathit{OC}//\mathit{BD}$

B．

$\mathit{AD}\perp \mathit{OC}$

C．

$\mathit{\Delta CEF}\cong \mathit{\Delta BED}$

D．

$\mathit{AF}=\mathit{FD}$

已知抛物线 $y=x^2-1$ 与 $y$ 轴交于点 $A$ ，与直线 $y=\mathit{kx}(k$ 为任意实数）相交于 $B$ ， $C$ 两点，则下列结论不正确的是 $($ 　　 $)$

A．	存在实数 $k$ ，使得 $\mathit{\Delta ABC}$ 为等腰三角形
B．	存在实数 $k$ ，使得 $\mathit{\Delta ABC}$ 的内角中有两角分别为 $30°$ 和 $60°$
C．	任意实数 $k$ ，使得 $\mathit{\Delta ABC}$ 都为直角三角形
D．	存在实数 $k$ ，使得 $\mathit{\Delta ABC}$ 为等边三角形

如图， $\mathit{AB}//\mathit{CD}$ ， $\mathit{AD}=\mathit{CD}$ ， $\angle 1=50°$ ，则 $\angle 2$ 的度数是 $($ 　　 $)$

A．

$55°$

B．

$60°$

C．

$65°$

D．

$70°$

一个等腰三角形的底边长是6，腰长是一元二次方程 $x^2-8x+15=0$ 的一根，则此三角形的周长是 $($ 　　 $)$

A．

16

B．

12

C．

14

D．

12或16