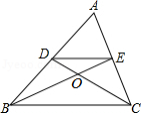
如图,在 中, , 分别为 , 的中点, 交 于点 ,连接 .有下列结论:① ;② ;③ ;④ 的延长线经过 的中点.其中正确的是 (填写所有正确结论的编号)
如图, 、 , 、 分别为矩形 的边 、 、 、 的中点,连接 、 、 , , .已知 , ,则 的长为 .

如图, 中,点 为边 的中点,连接 ,将 沿直线 翻折至 所在平面内,得 ,连接 ,分别与边 交于点 ,与 交于点 .若 , ,则 的长为 .

如图,在矩形 中, , ,点 在 上, ,点 是边 上一动点,以 为斜边作 .若点 在矩形 的边上,且这样的直角三角形恰好有两个,则 的值是 .

试题篮
()