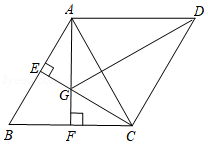
如图, 中, , , ,将 沿过点 的直线 折叠,使点 落到 边上的点 处,折痕交 边于点 .
(1)求证:四边形 是菱形;
(2)若点 是直线 上的一个动点,请计算 的最小值.

下列说法:
①四边相等的四边形一定是菱形
②顺次连接矩形各边中点形成的四边形一定是正方形
③对角线相等的四边形一定是矩形
④经过平行四边形对角线交点的直线,一定能把平行四边形分成面积相等的两部分
其中正确的有 个.
A.4B.3C.2D.1
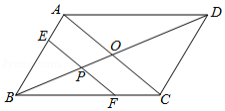
如图,在平行四边形 中, 、 分别是 、 的中点, ,垂足为 , ,垂足为 , 与 相交于点 .
(1)证明: .
(2)若 ,求四边形 的对角线 的长.
如图,在平行四边形 中,按以下步骤作图:①以 为圆心,任意长为半径作弧,分别交 , 于点 , ;②分别以 , 为圆心,以大于 的长为半径作弧,两弧相交于点 ;③作 射线,交边 于点 ,若 , ,则平行四边形 周长为 .

如图,平行四边形 的对角线 、 相交于点 , 平分 ,分别交 、 于点 、 ,连接 , , ,则下列结论:
① ② ③ ④ ⑤ ,正确的个数是
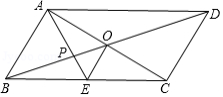
A.2B.3C.4D.5
如图,平行四边形 的对角线 、 相交于点 , 平分 ,分别交 、 于点 、 ,连接 , , ,则下列结论:
① ② ③ ④ ⑤ ,正确的个数是

A.2B.3C.4D.5
如图,在平行四边形 中,对角线 、 相交于点 , ,点 、点 分别是 、 的中点,连接 , , 于点 , 交 于点 , ,则线段 的长为 .

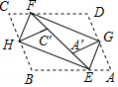
如图,平行四边形纸片 的边 , 的长分别是 和 ,将其四个角向内对折后,点 与点 重合于点 ,点 与点 重合于点 .四条折痕围成一个“信封四边形” ,其顶点分别在平行四边形 的四条边上,则 .
如图,平行四边形 中,对角线 、 相交于点 ,且 , , 是对角线 上任意一点,过点 作 ,与平行四边形的两条边分别交于点 、 .设 , ,则能大致表示 与 之间关系的图象为
A.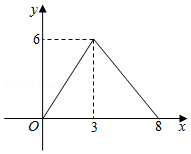
B.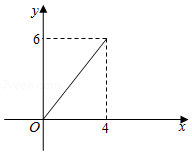
C.
D.
平行四边形 中, 、 是两条对角线,现从以下四个关系① ;② ;③ ;④ 中随机取出一个作为条件,即可推出平行四边形 是菱形的概率为
A. B. C. D.1
如图,抛物线 与 轴交于 , 两点,与 轴交于点 ,顶点为 ,以 为直径作 .下列结论:①抛物线的对称轴是直线 ;② 的面积为 ;③抛物线上存在点 ,使四边形 为平行四边形;④直线 与 相切.其中正确结论的个数是

A.1B.2C.3D.4
试题篮
()