初中数学菱形的性质选择题

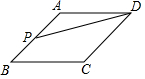
如图，点 P是菱形 ABCD边上的一动点，它从点 A出发沿在 A→ B→ C→ D路径匀速运动到点 D，设△ PAD的面积为 y， P点的运动时间为 x，则 y关于 x的函数图象大致为（　　）

A．		B．
C．		D．

一个菱形的边长是方程 x ²﹣8 x+15＝0的一个根，其中一条对角线长为8，则该菱形的面积为（　　）

A．

48

B．

24

C．

24或40

D．

48或80

已知菱形的边长为3，较短的一条对角线的长为2，则该菱形较长的一条对角线的长为（　　）

A．

2 $\sqrt{2}$

B．

2 $\sqrt{5}$

C．

4 $\sqrt{2}$

D．

2 $\sqrt{10}$

如图，矩形 ABCD与菱形 EFGH的对角线均交于点 O，且 EG∥ BC，将矩形折叠，使点 C与点 O重合，折痕 MN过点 G．若 AB＝ $\sqrt{6}$ ， EF＝2，∠ H＝120°，则 DN的长为（　　）

A．

$\sqrt{6}$ - $\sqrt{3}$

B．

$\frac{\sqrt{6}+\sqrt{3}}{2}$

C．

$\frac{\sqrt{3}}{2}$

D．

2 $\sqrt{3}-\sqrt{6}$

如图，菱形 ABCD周长为20，对角线 AC、 BD相交于点 O， E是 CD的中点，则 OE的长是（　　）

A．

2.5

B．

3

C．

4

D．

5

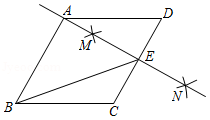
如图，在菱形 ABCD中，按以下步骤作图：

①分别以点 C和点 D为圆心，大于 $\frac{1}{2}$ CD为半径作弧，两弧交于点 M， N；

②作直线 MN，且 MN恰好经过点 A，与 CD交于点 E，连接 BE，

则下列说法错误的是（　　）

A．	∠ABC＝60°	B．	S △ ABE＝2S △ ADE
C．	若AB＝4，则BE＝ $4\sqrt{7}$	D．	sin∠CBE＝ $\frac{\sqrt{21}}{14}$

如图，菱形ABCD的边AB＝8，∠B＝60°，P是AB上一点，BP＝3，Q是CD边上一动点，将梯形APQD沿直线PQ折叠，A的对应点A′．当CA′的长度最小时，CQ的长为（　　）

A．5B．7C．8D． $\frac{13}{2}$

如图，将边长为4的菱形 ABCD纸片折叠，使点 A恰好落在对角线的交点 O处，若折痕 EF＝2 $\sqrt{3}$ ，则∠ A＝（　　）

A．

120°

B．

100°

C．

60°

D．

30°

菱形具有而一般平行四边形不具有的性质是　　

A．对边相等B．对角相等

C．对角线互相平分D．对角线互相垂直

菱形具有而一般平行四边形不具有的性质是　　

A．对边相等B．对角相等

C．对角线互相平分D．对角线互相垂直

如图，在周长为12的菱形中，，，若为对角线上一动点，则的最小值为　　

A．1B．2C．3D．4

如图，在菱形 $\mathit{ABCD}$ 中， $\angle B=60°$ ， $\mathit{AB}=2$ ．动点 $P$ 从点 $B$ 出发，以每秒1个单位长度的速度沿折线 $\mathit{BA}\to \mathit{AC}$ 运动到点 $C$ ，同时动点 $Q$ 从点 $A$ 出发，以相同速度沿折线 $\mathit{AC}\to \mathit{CD}$ 运动到点 $D$ ，当一个点停止运动时，另一点也随之停止．设 $\mathit{\Delta APQ}$ 的面积为 $y$ ，运动时间为 $x$ 秒．则下列图象能大致反映 $y$ 与 $x$ 之间函数关系的是 $($ 　　 $)$

A．		B．
C．		D．

如图，在菱形 $\mathit{ABCD}$ 中， $\angle B=60°$ ， $\mathit{AB}=2$ ．动点 $P$ 从点 $B$ 出发，以每秒1个单位长度的速度沿折线 $\mathit{BA}\to \mathit{AC}$ 运动到点 $C$ ，同时动点 $Q$ 从点 $A$ 出发，以相同速度沿折线 $\mathit{AC}\to \mathit{CD}$ 运动到点 $D$ ，当一个点停止运动时，另一点也随之停止．设 $\mathit{\Delta APQ}$ 的面积为 $y$ ，运动时间为 $x$ 秒．则下列图象能大致反映 $y$ 与 $x$ 之间函数关系的是 $($ 　　 $)$

A．		B．
C．		D．

如图，在菱形 $\mathit{ABCD}$ 中， $P$ 是对角线 $\mathit{AC}$ 上一动点，过点 $P$ 作 $\mathit{PE}\perp \mathit{BC}$ 于点 $E$ ． $\mathit{PF}\perp \mathit{AB}$ 于点 $F$ ．若菱形 $\mathit{ABCD}$ 的周长为20，面积为24，则 $\mathit{PE}+\mathit{PF}$ 的值为 $($ 　　 $)$

A．

4

B．

$\frac{24}{5}$

C．

6

D．

$\frac{48}{5}$

如图，四边形 $\mathit{ABCD}$ 是菱形，对角线 $\mathit{AC}$ ， $\mathit{BD}$ 相交于点 $O$ ， $\mathit{AC}=8$ ． $\mathit{BD}=6$ ，点 $E$ 是 $\mathit{CD}$ 上一点，连接 $\mathit{OE}$ ，若 $\mathit{OE}=\mathit{CE}$ ，则 $\mathit{OE}$ 的长是 $($ 　　 $)$

A．

2

B．

$\frac{5}{2}$

C．

3

D．

4