如图,公园内有一个半径为20米的圆形草坪, , 是圆上的点, 为圆心, ,从 到 只有路 ,一部分市民为走“捷径”,踩坏了花草,走出了一条小路 .通过计算可知,这些市民其实仅仅少走了 步(假设1步为0.5米,结果保留整数).(参考数据: , 取

已知:如图, 内接于 ,且半径 ,点 在半径 的延长线上,且 , ,则由 ,线段 和线段 所围成图形的阴影部分的面积为 .

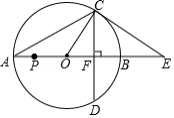
如图,以 为直径的 与 相切于点 , 交 的延长线于点 ,直径 , ,弦 ,垂足为点 ,连接 , ,则下列结论正确的是 .(写出所有正确结论的序号)
① ;
②扇形 的面积为 ;
③ ;
④若点 为线段 上一动点,则 有最大值20.25.
如图是由两个长方形组成的工件平面图(单位: ,直线 是它的对称轴,能完全覆盖这个平面图形的圆面的最小半径是 .

试题篮
()