如图1,在矩形纸片ABCD中, ,其中m≥1,将该矩形沿EF折叠(点E、F分别在边AB、CD上),使点B落在AD边上的点M处,点C落在点N处,MN与CD相交于点P,连接EP.设
,其中m≥1,将该矩形沿EF折叠(点E、F分别在边AB、CD上),使点B落在AD边上的点M处,点C落在点N处,MN与CD相交于点P,连接EP.设 ,其中0<n≤1.
,其中0<n≤1.
(1)如图2,当 (即M点与D点重合),
(即M点与D点重合), 时,则
时,则 ;
;
(2)如图3,当 (M为AD的中点),m的值发生变化时,求证:
(M为AD的中点),m的值发生变化时,求证: ;
;
(3)如图1,当 ,n的值发生变化时,
,n的值发生变化时, 的值是否发生变化?说明理由.
的值是否发生变化?说明理由.
如图(1),抛物线 与x轴交于A、B两点,与y轴交于点C,其中点A的坐标为(﹣2,0).
与x轴交于A、B两点,与y轴交于点C,其中点A的坐标为(﹣2,0).
(1)求此抛物线的解析式;
(2)①若点D是第一象限内抛物线上的一个动点,过点D作DE⊥x轴于E,连接CD,以OE为直径作⊙M,如图(2),试求当CD与⊙M相切时D点的坐标;
②点F是x轴上的动点,在抛物线上是否存在一点G,使A、C、G、F四点为顶点的四边形是平行四边形?若存在,求出点G的坐标;若不存在,请说明理由.
(1)如图1,在正方形ABCD中,E是AB上一点,F是AD延长线上一点,且DF=BE.求证:CE=CF;
(2)如图2,在正方形ABCD中,E是AB上一点,G是AD上一点,如果∠GCE=45°,请你利用(1)的结论证明:GE=BE+GD;
(3)运用(1)(2)解答中所积累的经验和知识,完成下题:
如图3,在直角梯形ABCD中,AD∥BC,(BC>AD),∠B=90°,AB=BC,E是AB上一点,且∠DCE=45°,BE=4,DE=10,求直角梯形ABCD的面积.
已知,在矩形ABCD中,E为BC边上一点,AE⊥DE,AB=12,BE=16,F为线段BE上一点,EF=7,连接AF.如图①,现有一张硬质纸片△GMN,∠NGM=90°,NG=6,MG=8,斜边MN与边BC在同一直线上,点N与点E重合,点G在线段DE上.如图②,△GMN从图①的位置出发,以每秒1个单位的速度沿EB向点B匀速移动,同时,点P从A点出发,以每秒1个单位的速度沿AD向点D匀速移动,点Q为直线GN与线段AE的交点,连接PQ.当点N到达终点B时,△GMN和点P同时停止运动.设运动时间为t秒,解答下列问题:
(1)在整个运动过程中,当点G在线段AE上时,求t的值.
(2)在整个运动过程中,是否存在点P,使△APQ是等腰三角形.若存在,求出t的值;若不存在,说明理由.
(3)在整个运动过程中,设△GMN与△AEF重叠部分的面积为S,请直接写出S与t之间的函数关系式以及自变量t的取值范围.
正方形ABCD的顶点A在直线MN上,点O是对角线AC、BD的交点,过点O作OE⊥MN于点E,过点B作BF⊥MN于点F.
(1)如图1,当O、B两点均在直线MN上方时,易证:AF+BF=2OE(不需证明)
(2)当正方形ABCD绕点A顺时针旋转至图2、图3的位置时,线段AF、BF、OE之间又有怎样的关系?请直接写出你的猜想,并选择一种情况给予证明.
如图1,在矩形ABCD中,AB=4,AD=2,点P是边AB上的一个动点(不与点A、点B重合),点Q在边AD上,将△CBP和△QAP分别沿PC、PQ折叠,使B点与E点重合,A点与F点重合,且P、E、F三点共线.
(1)若点E平分线段PF,则此时AQ的长为多少?
(2)若线段CE与线段QF所在的平行直线之间的距离为2,则此时AP的长为多少?
(3)在“线段CE”、“线段QF”、“点A”这三者中,是否存在两个在同一条直线上的情况?若存在,求出此时AP的长;若不存在,请说明理由.

已知:在梯形ABCD中,CD∥AB,AD=DC=BC=2,AB=4.点M从A开始,以每秒1个单位的速度向点B运动;点N从点C出发,沿C→D→A方向,以每秒1个单位的速度向点A运动,若M、N同时出发,其中一点到达终点时,另一个点也停止运动.运动时间为t秒,过点N作NQ⊥CD交AC于点Q.
(1)设△AMQ的面积为S,求S与t的函数关系式,并写出t的取值范围.
(2)在梯形ABCD的对称轴上是否存在点P,使△PAD为直角三角形?若存在,求点P到AB的距离;若不存在,说明理由.
(3)在点M、N运动过程中,是否存在t值,使△AMQ为等腰三角形?若存在,求出t值;若不存在,说明理由.
如图,将正方形对折后展开(图④是连续两次对折后再展开),再按图示方法折叠,能够得到一个直角三角形(阴影部分),且它的一条直角边等于斜边的一半.这样的图形有
图① 图② 图③ 图④
| A.4个 | B.3个 | C.2个 | D.1个 |
阅读下面材料:
小明遇到这样一个问题:如图1,在边长为 的正方形ABCD各边上分别截取AE=BF=CG=DH=1,当∠AFQ=∠BGM=∠CHN=∠DEP=45°时,求正方形MNPQ的面积.小明发现:分别延长QE,MF,NG,PH,交FA,GB,HC,ED的延长线于点R,S,T,W,可得△RQF,△SMG,△TNH,△WPE是四个全等的等腰直角三角形(如图2)
的正方形ABCD各边上分别截取AE=BF=CG=DH=1,当∠AFQ=∠BGM=∠CHN=∠DEP=45°时,求正方形MNPQ的面积.小明发现:分别延长QE,MF,NG,PH,交FA,GB,HC,ED的延长线于点R,S,T,W,可得△RQF,△SMG,△TNH,△WPE是四个全等的等腰直角三角形(如图2)

请回答:
(1)若将上述四个等腰直角三角形拼成一个新的正方形(无缝隙,不重叠),则这个新的正方形的边长为__________;
(2)求正方形MNPQ的面积.
参考小明思考问题的方法,解决问题:
如图3,在等边△ABC各边上分别截取AD=BE=CF,再分别过点D,E,F作BC,AC,AB的垂线,得到等边△RPQ,若 ,则AD的长为__________.
,则AD的长为__________.
在正方形 外侧作直线
外侧作直线 ,点
,点 关于直线
关于直线 的对称点为
的对称点为 ,连接
,连接 ,其中
,其中 交直线
交直线 于点
于点 .
.
(1)依题意补全图1;
(2)若 ,求
,求 的度数;
的度数;
(3)如图2,若 ,用等式表示线段
,用等式表示线段 之间的数量关系,并证明.
之间的数量关系,并证明.

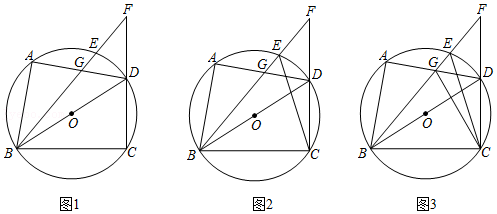
如图1,四边形 内接于 , 为直径, 上存在点 ,满足 ,连结 并延长交 的延长线于点 , 与 交于点 .
(1)若 ,请用含 的代数式表示 .
(2)如图2,连结 , .求证: .
(3)如图3,在(2)的条件下,连结 , .
①若 ,求 的周长.
②求 的最小值.
如图1,矩形ABCD中,AB=2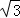 ,BC=6,点P、Q分别是线段AD和线段BC上的动点,满足∠PQB=60°.
,BC=6,点P、Q分别是线段AD和线段BC上的动点,满足∠PQB=60°.
(1)填空:①∠ACB= 度;②PQ= .
(2)设线段BC的中点为N,PQ与线段AC相交于点M,若△CMN为直角三角形,请直接写出满足条件的AP的长度.
(3)设AP=x,△PBQ与△ABC的重叠部分的面积为S,试求S与x的函数关系式和自变量x的取值范围.
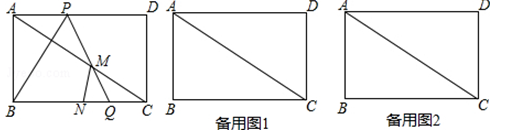
(本题8分)如图,在□ABCD中, 、
、 是
是 、
、 的中点,
的中点, 、
、 的延长线分别交
的延长线分别交 、
、 的延长线于
的延长线于 、
、 ;
;
(1)求证:BH=AB;
(2)若四边形 为菱形,试判断
为菱形,试判断 与
与 的大小,并证明你的结论.
的大小,并证明你的结论.
在平面直角坐标系xOy中,对于任意三点A,B,C,给出如下定义:
若矩形的任何一条边均与某条坐标轴平行,且A,B,C三点都在矩形的内部或边界上,则称该矩形为点A,B,C的外延矩形.点A,B,C的所有外延矩形中,面积最小的矩形称为点A,B,C的最佳外延矩形.例如,图中的矩形 ,
,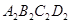 ,
,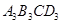 都是点A,B,C的外延矩形,矩形
都是点A,B,C的外延矩形,矩形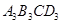 是点A,B,C的最佳外延矩形.
是点A,B,C的最佳外延矩形.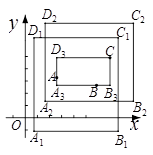
(1)如图1,已知A(-2,0),B(4,3),C(0,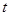 ).
).
①若 ,则点A,B,C的最佳外延矩形的面积为 ;
,则点A,B,C的最佳外延矩形的面积为 ;
②若点A,B,C的最佳外延矩形的面积为24,则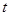 的值为 ;
的值为 ;
(2)如图2,已知点M(6,0),N(0,8).P(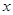 ,
,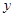 )是抛物线
)是抛物线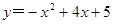 上一点,求点M,N,P的最佳外延矩形面积的最小值,以及此时点P的横坐标
上一点,求点M,N,P的最佳外延矩形面积的最小值,以及此时点P的横坐标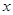 的取值范围;
的取值范围;
(3)如图3,已知点D(1,1).E(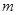 ,
,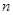 )是函数
)是函数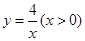 的图象上一点,矩形OFEG是点O,D,E的一个面积最小的最佳外延矩形,⊙H是矩形OFEG的外接圆,请直接写出⊙H的半径r的取值范围.
的图象上一点,矩形OFEG是点O,D,E的一个面积最小的最佳外延矩形,⊙H是矩形OFEG的外接圆,请直接写出⊙H的半径r的取值范围.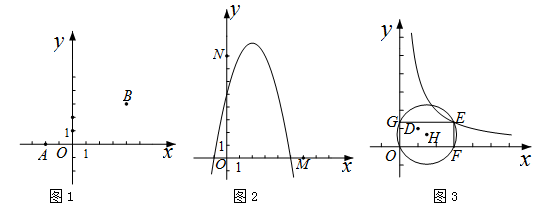
试题篮
()