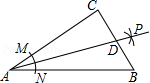
如图,在 中, 是 上一点,延长 到点 ,使 .
(1)求证: ;
(2)用直尺和圆规在 上作出一点 ,使 (保留作图的痕迹,不写作法).

如图,在 中, ,以顶点 为圆心,适当长为半径画弧,分别交 , 于点 , ,再分别以点 , 为圆心,大于 的长为半径画弧,两弧交于点 ,作射线 交边 于点 ,若 , ,则 的面积是
A.15B.30C.45D.60
如图,四边形 是平行四边形,以点 为圆心、 的长为半径画弧交 于点 ,再分别以点 , 为圆心、大于 的长为半径画弧,两弧交于点 ,作射线 交 于点 ,连接 .下列结论中不一定成立的是

A. B. C. 平分 D.
如图, 是 的对角线,按以下步骤作图:①分别以点 和点 为圆心,
大于 的长为半径作弧,两弧相交于 , 两点;②作直线 ,分别交 , 于点 , ,连接 , .若 , ,则 的边 上的高为 .

如图,点 在 的边 上,用尺规作出了 ,作图痕迹中, 是

A.以点 为圆心、 的长为半径的弧
B.以点 为圆心、 的长为半径的弧
C.以点 为圆心、 的长为半径的弧
D.以点 为圆心、 的长为半径的弧
如图, 是矩形 的对角线,在 和 上分别截取 , ,使 ;分别以 , 为圆心,以大于 的长为半径作弧,两弧在 内交于点 ,作射线 交 于点 ,若 ,则点 到 的距离为 .

如图, 平分 , 是边 上一点,以点 为圆心、大于点 到 的距离为半径作弧,交 于点 、 ,再分别以点 、 为圆心,大于 的长为半径作弧,两弧交于点 、作直线 分别交 、 于点 、 .若 , ,则 .
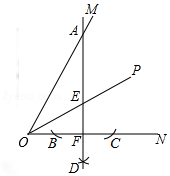
如图, 中, , ,连接 ,分别以点 和点 为圆心,大于 的长为半径作弧,两弧相交于点 , ,作直线 ,交 于点 ,连接 ,则 的周长是 .

如图,在 中, , , .按以下步骤作图:
①以 为圆心,任意长为半径作弧,分别交 , 于点 , ;
②分别以 , 为圆心,以大于 的长为半径作弧,两弧相交于点 ;
③作射线 ;
④以同样的方法作射线 .
交 于点 ,连接 ,则 .

如图, ,以点 为圆心,以任意长为半径作弧交 , 于 , 两点;分别以 , 为圆心,以大于 的长为半径作弧,两弧相交于点 ;以 为端点作射线 ,在射线 上截取线段 ,则 点到 的距离为

A.6B.2C.3D.
如图所示,已知 ,现按照以下步骤作图:
①在 , 上分别截取线段 , ,使 ;
②分别以 , 为圆心,以大于 的长为半径画弧,在 内两弧交于点 ;
③作射线 .
则 的大小为 .

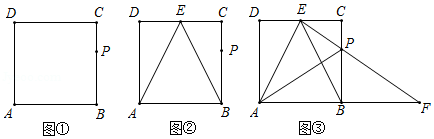
如图,在矩形 中, , , 是 边上的一点,且 .
(1)用尺规在图①中作出 边上的中点 ,连接 、 (保留作图痕迹,不写作法);
(2)如图②,在(1)的条件下,判断 是否平分 ,并说明理由;
(3)如图③,在(2)的条件下,连接 并延长交 的延长线于点 ,连接 ,不添加辅助线, 能否由都经过 点的两次变换与 组成一个等腰三角形?如果能,说明理由,并写出两种方法(指出对称轴、旋转中心、旋转方向和平移距离)
如图, 是 的外接圆, 是 的直径, .
(1)利用尺规,作 的平分线,交 于点 ;(保留作图痕迹,不写作法)
(2)在(1)的条件下,连接 , ,若 ,求 的度数;
(3)在(2)的条件下, 交 于点 ,求由线段 , , 所围成区域的面积.(其中 表示劣弧,结果保留 和根号)

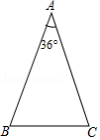
如图,已知等腰 顶角 .
(1)在 上作一点 ,使 (要求:尺规作图,保留作图痕迹,不必写作法和证明,最后用黑色墨水笔加黑);
(2)求证: 是等腰三角形.
试题篮
()