如图,在Rt△ABC中,∠ACB=90°,AC="4" cm ,BC="3" cm,⊙O为△ABC的内切圆.
(1)求⊙O的半径;
(2)点P从点B沿边BA向点A以点1cm/s 的速度匀速运动,以点P为圆心,PB长为半径作圆.设点P运动的时间为 t s.若⊙P与⊙O相切,求t的值.
如图,Rt△ABC中,∠ACB=90°,AC=6 cm,BC=8 cm,动点P从点B出发,在BA边上以每秒5 cm的速度向点A匀速运动,同时动点Q从点C出发,在CB边上以每秒4 cm的速度向点B匀速运动,运动时间为t秒(0<t<2),连接PQ.
(1)若△BPQ与△ABC相似,求t的值;
(2)连接AQ、CP,若AQ⊥CP,求t的值;
(3)试证明:PQ的中点在△ABC的一条中位线上.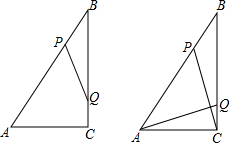
把两块全等的直角三角形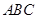 和
和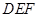 叠放在一起,使三角板
叠放在一起,使三角板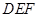 的锐角顶点
的锐角顶点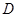 与三角板
与三角板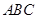 的斜边中点
的斜边中点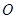 重合,其中
重合,其中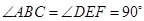 ,
,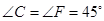 ,
,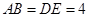 ,把三角板
,把三角板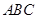 固定不动,让三角板
固定不动,让三角板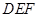 绕点
绕点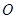 旋转,设射线
旋转,设射线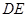 与射线
与射线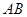 相交于点
相交于点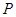 ,射线
,射线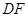 与线段
与线段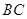 相交于点
相交于点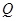 .
.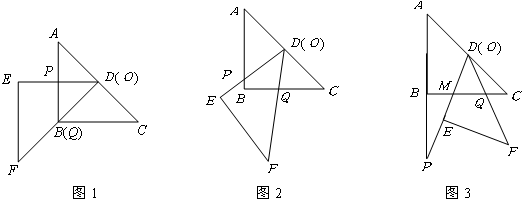
(1)如图1,当射线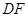 经过点
经过点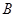 ,即点
,即点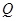 与点
与点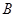 重合时,易证
重合时,易证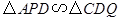 .此时,
.此时,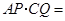 ;将三角板
;将三角板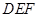 由图1所示的位置绕点
由图1所示的位置绕点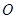 沿逆时针方向旋转,设旋转角为
沿逆时针方向旋转,设旋转角为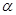 .其中
.其中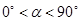 ,问
,问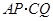 的值是否改变?答: (填“会”或“不会”);若改变,
的值是否改变?答: (填“会”或“不会”);若改变,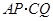 的值为 (不必说明理由);
的值为 (不必说明理由);
(2)在(1)的条件下,设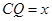 ,两块三角板重叠面积为
,两块三角板重叠面积为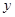 ,求
,求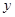 与
与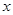 的函数关系式.(图2,图3供解题用)
的函数关系式.(图2,图3供解题用)
如图,在反比例函数 位于第一象限内的图象上取一点P1,连结OP1,作P1A1^x轴,垂足为A1,在OA1的延长线上截取A1 B1= OA1,过B1作OP1的平行线,交反比例函数
位于第一象限内的图象上取一点P1,连结OP1,作P1A1^x轴,垂足为A1,在OA1的延长线上截取A1 B1= OA1,过B1作OP1的平行线,交反比例函数 的图象于P2,过P2作P2A2^x轴,垂足为A2,在OA2的延长线上截取A2 B2= B1A2,连结P1 B1,P2 B2,则
的图象于P2,过P2作P2A2^x轴,垂足为A2,在OA2的延长线上截取A2 B2= B1A2,连结P1 B1,P2 B2,则 的值是 .
的值是 .
已知:把Rt△ABC和Rt△DEF按如图(1)摆放(点C与点E重合),点B、C(E)、F在同一条直线上.∠ACB = ∠EDF = 90°,∠DEF = 45°,AC =" 8" cm,BC =" 6" cm,EF =" 9" cm。
如图(2),△DEF从图(1)的位置出发,以1 cm/s的速度沿CB向△ABC匀速移动,在△DEF移动的同时,点P从△ABC的顶点B出发,以2 cm/s的速度沿BA向点A匀速移动。当△DEF的顶点D移动到AC边上时,△DEF停止移动,点P也随之停止移。DE与AC相交于点Q,连接PQ,设移动时间为t(s)(0<t<4.5)。解答下列问题:
(1)当t为何值时,点A在线段PQ的垂直平分线上?
(2)连接PE,设四边形APEC的面积为y(cm2),求y与t之间的函数关系式;是否存在某一时刻t,使面积y最小?若存在,求出y的最小值;若不存在,说明理由。
(3)是否存在某一时刻t,使P、Q、F三点在同一条直线上?若存在,求出此时t的值;若不存在,说明理由。(图(3)供同学们做题使用)
如图,在平面直角坐标系中,△ABC 的顶点坐标分别为A(-2,0)、B(4,0)、C(0,2).
(1)请用尺规作出△ABC的外接圆⊙P(保留作图痕迹,不写作法);
(2)求出(1)中外接圆圆心P的坐标;
(3)⊙P上是否存在一点Q,使得△QBC与△AOC相似?如果存在,请直接写出点Q 坐标;如果不存在,请说明理由.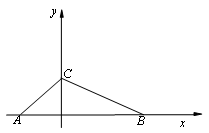
在△ABC中,AB=6,BC=8,∠ACB=30°,将△ABC绕点B按逆时针方向旋转,得到△A1BC1.
(1)如图1,当点C1在线段CA的延长线上时,求∠CC1A1的度数;
(2)如图2,连接AA1,CC1,若△CBC1的面积为16,求△ABA1的面积;
(3)如图3,点E为线段AB中点,点P是线段AC上的动点,在△ABC绕点B按逆时针方向旋转的过程中,点P的对应点是点P1,直接写出线段EP1长度的最大值与最小值.
如图1,在直角梯形ABCD中,AD∥BC,∠A=90°,BD⊥DC,BC=10cm,CD=6cm.在线段BC、CD上有动点F、E,点F以每秒2cm的速度,在线段BC上从点B向点C匀速运动;同时点E以每秒1cm的速度,在线段CD上从点C向点D匀速运动.当点F到达点C时,点E同时停止运动.设点F运动的时间为t(秒).
(1)求AD的长;
(2)设四边形BFED的面积为y,求y 关于t的函数关系式并写出自变量的取值范围
(3)当t为何的值时,以EE为半径的⊙F与CD边只有一个公共点.
已知:把Rt△ABC和Rt△DEF按如图(1)摆放(点C与点E重合),点B、C(E)、F在同一条直线上.∠ACB = ∠EDF = 90°,∠DEF = 45°,AC =" 8" cm,BC =" 6" cm,EF =" 9" cm。
如图(2),△DEF从图(1)的位置出发,以1 cm/s的速度沿CB向△ABC匀速移动,在△DEF移动的同时,点P从△ABC的顶点B出发,以2 cm/s的速度沿BA向点A匀速移动。当△DEF的顶点D移动到AC边上时,△DEF停止移动,点P也随之停止移。DE与AC相交于点Q,连接PQ,设移动时间为t(s)(0<t<4.5)。解答下列问题:
(1)当t为何值时,点A在线段PQ的垂直平分线上?
(2)连接PE,设四边形APEC的面积为y(cm2),求y与t之间的函数关系式;是否存在某一时刻t,使面积y最小?若存在,求出y的最小值;若不存在,说明理由。
(3)是否存在某一时刻t,使P、Q、F三点在同一条直线上?若存在,求出此时t的值;若不存在,说明理由。(图(3)供同学们做题使用)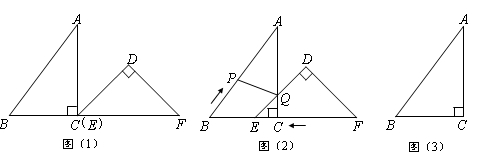
如图14-1,在锐角△ABC中,AB = 5,AC = ,∠ACB = 45°.
,∠ACB = 45°.
计算:求BC的长;
操作:将图14-1中的△ABC绕点B按逆时针方向旋转,得到△A1BC1.如图14-2,当点C1在线段CA的延长线上时.
(1)证明:A1C1⊥CC1;
(2)求四边形A1BCC1的面积;



探究:
将图14-1中的△ABC绕点B按逆时针方向旋转,得到△A1BC1.连结AA1,CC1,如图14-3.若△ABA1的面积为5,求点C到BC1的距离;
拓展:
将图14-1中的△ABC绕点B按逆时针方向旋转,得到△A1BC1.点E为线段AB中点,点P是线段AC上的动点,在△ABC绕点B按逆时针方向旋转过程中,点P的对应点是点P1,如图14-4.
(1)若点P是线段AC的中点,求线段EP1长度的最大值与最小值;
(2)若点P是线段AC上的任一点,直接写出线段EP1长度的最大值与最小值.
已知:△ABD和△CBD关于直线BD对称(点A的对称点是点C),点E、F分别是线段BC和线段BD上的点,且点F在线段EC的垂直平分线上,连接AF、AE,AE交BD于点G.
(1)如图l,求证:∠EAF=∠ABD;
(2)如图2,当AB=AD时,M是线段AG上一点,连接BM、ED、MF,MF的延长线交ED于点N,∠MBF= ∠BAF,AF=
∠BAF,AF= AD,请你判断线段FM和FN之间的数量关系,并证明你的判断是正确的.
AD,请你判断线段FM和FN之间的数量关系,并证明你的判断是正确的.
如图,正方形ABCD的边长为3,点E,F分别在边AB,BC上,AE=BF=1,小球P从点E出发沿直线向点F运动,每当碰到正方形的边时反弹,反弹时反射角等于入射角.当小球P第一次碰到BC边时,小球P所经过的路程为 ;当小球P第一次碰到AD边时,小球P所经过的路程为 ;当小球P第n(n为正整数)次碰到点F时,小球P所经过的路程为 .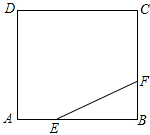
如图①,在□ABCD中,对角线AC⊥AB,BC=10,tan∠B=2.点E是BC边上的动点,过点E作EF⊥BC于点E,交折线AB-AD于点F,以EF为边在其右侧作正方形EFGH,使EH边落在射线BC上.点E从点B出发,以每秒1个单位的速度在BC边上运动,当点E与点C重合时,点E停止运动,设点E的运动时间为t(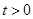 )秒.
)秒.
(1)□ABCD的面积为 ;当t= 秒时,点F与点A重合;
(2)点E在运动过程中,连接正方形EFGH的对角线EG,得△EHG,设△EHG与△ABC的重叠部分面积为S,请直接写出S与t的函数关系式以及对应的自变量t的取值范围;
(3)作点B关于点A的对称点Bˊ,连接CBˊ交AD边于点M(如图②),当点F在AD边上时,EF与对角线AC交于点N,连接MN得△MNC.是否存在时间t,使△MNC为等腰三角形?若存在,请求出使△MNC为等腰三角形的时间t;若不存在,请说明理由.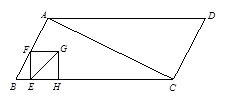
如图1,□ABCD中,对角线BD⊥AB,AB=5,AD边上的高为 .等腰直角△EFG中,EF=4, ∠EGF=45°,且△EFG与□ABCD位于直线AD的同侧,点F与点D重合,GF与AD在同一直线上.△EFG从点D出发以每秒1个单位的速度沿射线DA方向平移,当点G到点A时停止运动;同时点P也从点A出发,以每秒3个单位的速度沿折线AD→DC方向运动,到达点C时停止运动,设运动的时间为t.
.等腰直角△EFG中,EF=4, ∠EGF=45°,且△EFG与□ABCD位于直线AD的同侧,点F与点D重合,GF与AD在同一直线上.△EFG从点D出发以每秒1个单位的速度沿射线DA方向平移,当点G到点A时停止运动;同时点P也从点A出发,以每秒3个单位的速度沿折线AD→DC方向运动,到达点C时停止运动,设运动的时间为t.
(1)求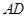 的长度;
的长度;
(2)在 平移的过程中,记
平移的过程中,记 与
与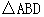 相互重叠的面积为
相互重叠的面积为 ,请直接写出面积
,请直接写出面积 与运动时间
与运动时间 的函数关系式,并写出
的函数关系式,并写出 的取值范围;
的取值范围;
(3)如图2,在运动的过程中,若线段 与线段
与线段 交于点
交于点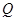 ,连接
,连接 .是否存在这样的时间
.是否存在这样的时间 ,使得
,使得 为等腰三角形?若存在,求出对应的
为等腰三角形?若存在,求出对应的 值;若不存在,请说明理由.
值;若不存在,请说明理由.

如图①,在□ABCD中,对角线AC⊥AB,BC=10,tan∠B=2.点E是BC边上的动点,过点E作EF⊥BC于点E,交折线AB-AD于点F,以EF为边在其右侧作正方形EFGH,使EH边落在射线BC上.点E从点B出发,以每秒1个单位的速度在BC边上运动,当点E与点C重合时,点E停止运动,设点E的运动时间为t( )秒.
)秒.
(1)□ABCD的面积为 ;当t= 秒时,点F与点A重合;
(2)点E在运动过程中,连接正方形EFGH的对角线EG,得△EHG,设△EHG与△ABC的重叠部分面积为S,请直接写出S与t的函数关系式以及对应的自变量t的取值范围;
(3)作点B关于点A的对称点Bˊ,连接CBˊ交AD边于点M(如图②),当点F在AD边上时,EF与对角线AC交于点N,连接MN得△MNC.是否存在时间t,使△MNC为等腰三角形?若存在,请求出使△MNC为等腰三角形的时间t;若不存在,请说明理由.
试题篮
()