如图,□ABCD中,AC⊥AB.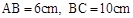 ,E是CD上的点,
,E是CD上的点,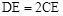 .点P从D点出发,以1cm/s的速度沿DA运动至A点停止.则当△EDP为等腰三角形时,点P的运动时间为 .
.点P从D点出发,以1cm/s的速度沿DA运动至A点停止.则当△EDP为等腰三角形时,点P的运动时间为 .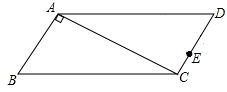
如图(1),将一个正六边形各边延长,构成一个正六角星形AFBDCE,它的面积为1;取△ABC和△DEF各边中点,连接成正六角星形A1F1B1D1C1E1,如图(2)中阴影部分;取△A1B1C1和△D1E1F1各边中点,连接成正六角星形A2F2B2D2C2E2,如图(3)中阴影部分;如此下去…,则正六角星形A4F4B4D4C4E4的面积为________.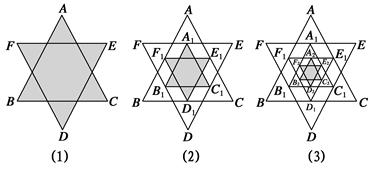
如图,点A1,A2,A3,A4,…,An在射线OA上,点B1,B2,B3,…,Bn―1在射线OB上,且A1B1∥A2B2∥A3B3∥…∥An﹣1Bn﹣1,A2B1∥A3B2∥A4B3∥…∥AnBn﹣1,△A1A2B1,△A2A3B2,…,△An﹣1AnBn﹣1为阴影三角形,若△A2B1B2,△A3B2B3的面积分别为1、4,则△A1A2B1的面积为__________;面积小于2014的阴影三角形共有__________个.
如图,△ABC是边长为1的等边三角形.取BC边中点E,作ED∥AB,EF∥AC,得到四边形EDAF,它的面积记作S1;取BE中点E1,作E1D1∥FB,E1F1∥EF,得到四边形E1D1FF1,它的面积记作S2.照此规律作下去,则S2014= . 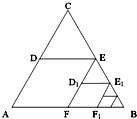
如图,长方形ABCD中,AB=4,AD=3,E是边AB上一点(不与A、B重合),F是边BC上一点(不与B、C重合).若△DEF和△BEF是相似三角形,则CF=.
如图,矩形纸片ABDC中,AB=5,AC=3,将纸片折叠,使点B落在边CD上的B′处,折痕为AE.在折痕A E上存在一点P到边CD的距离与到点B的距离相等,则此相等距离为__________.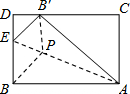
如图,在△ABC中,AB=AC,D、E是△ABC内两点,AD平分∠BAC,∠EBC=∠E=60°,若BE=6cm,DE=2cm,则BC=_________ .
如图,点G是Rt△ABC的重心,过点G作矩形GECF,当GF:GE=1:2时,则∠ B的正切值为.
已知点P是边长为4的正方形ABCD内一点,且PB="3" , BF⊥BP,垂足是点B, 若在射线BF上找一点M,使以点B, M, C为顶点的三角形与△ABP相似,则BM为___________.
在Rt△ABC中,∠C=90°, ,把这个直角三角形绕顶点C旋转后得到Rt△A'B'C,其中点B' 正好落在AB上,A'B'与AC相交于点D,那么
,把这个直角三角形绕顶点C旋转后得到Rt△A'B'C,其中点B' 正好落在AB上,A'B'与AC相交于点D,那么 .
.
在直角三角形ABC中, ,
, 是斜边AB的中点,过
是斜边AB的中点,过 作
作 于
于 ,连结
,连结 交
交 于
于 ;过
;过 作
作 于
于 ,连结
,连结 交
交 于
于 ;过
;过 作
作 于
于 ,…,如此继续,可以依次得到点
,…,如此继续,可以依次得到点 ,
, …,
…, ,分别记
,分别记 ,
, ,
, ,…,
,…, 的面积为
的面积为 ,
, ,
, ,…
,… ,则
,则 .
.
如图,在Rt△ABC中,∠ACB=90°,∠ABC=30°,直角∠MON的顶点O在AB上, OM、ON分别交CA、CB于点P、Q,∠MON绕点O任意旋转.当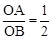 时,
时, 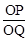 的值为;当
的值为;当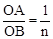 时,
时,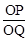 为.(用含n的式子表示)
为.(用含n的式子表示)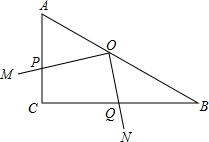
如图,Rt△ABC中,O为坐标原点,∠AOB=90°,∠B=30°,如果点A在反比例函数 (x>0)的图象上运动,那么点B在函数(填函数解析式)的图象上运动.
(x>0)的图象上运动,那么点B在函数(填函数解析式)的图象上运动.
如图1~4所示,每个图中的“7”字形是由若干个边长相等的正方形拼接而成,“7”字形的一个顶点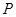 落在反比例函数
落在反比例函数 的图像上,另“7”字形有两个顶点落在
的图像上,另“7”字形有两个顶点落在 轴上,一个顶点落在
轴上,一个顶点落在 轴上.
轴上.
(1)图1中的每一个小正方形的面积是;
(2)按照图1 图2
图2 图3
图3 图4
图4
 这样的规律拼接下去,第
这样的规律拼接下去,第 个图形中每一个小正方形的面积是.(用含
个图形中每一个小正方形的面积是.(用含 的代数式表示)
的代数式表示)
试题篮
()