如图①,抛物线与
轴交于点
,与
轴交于点
,
,将直线
绕点
逆时针旋转
,所得直线与
轴交于点
.
(1)求直线的函数解析式;
(2)如图②,若点是直线
上方抛物线上的一个动点
①当点到直线
的距离最大时,求点
的坐标和最大距离;
②当点到直线
的距离为
时,求
的值.

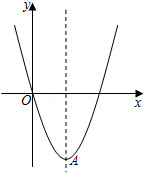
如图,在平面直角坐标系中,抛物线经过原点
,顶点为
.
(1)求抛物线的函数解析式;
(2)设点为抛物线
的对称轴上的一点,点
在该抛物线上,当四边
形为菱形时,求出点
的坐标;
(3)在(2)的条件下,抛物线在第一象限的图象上是否存在一点
,使得点
到直线
的距离与其到
轴的距离相等?若存在,求出直线
的函数解析式;若不存在,请说明理由.
如图,在平面直角坐标系中,抛物线经过原点
,顶点为
.
(1)求抛物线的函数解析式;
(2)设点为抛物线
的对称轴上的一点,点
在该抛物线上,当四边
形为菱形时,求出点
的坐标;
(3)在(2)的条件下,抛物线在第一象限的图象上是否存在一点
,使得点
到直线
的距离与其到
轴的距离相等?若存在,求出直线
的函数解析式;若不存在,请说明理由.

如图1,经过等边
的顶点
,
(圆心
在
内),分别与
,
的延长线交于点
,
,连结
,
交
于点
.
(1)求证:.
(2)当,
时,求
的长.
(3)设,
.
①求关于
的函数表达式;
②如图2,连结,
,若
的面积是
面积的10倍,求
的值.

如图1,已知在平面直角坐标系中,四边形
是矩形,点
,
分别在
轴和
轴的正半轴上,连结
,
,
,
是
的中点.
(1)求的长和点
的坐标;
(2)如图2,是线段
上的点,
,点
是线段
上的一个动点,经过
,
,
三点的抛物线交
轴的正半轴于点
,连结
交
于点
.
①将沿
所在的直线翻折,若点
恰好落在
上,求此时
的长和点
的坐标;
②以线段为边,在
所在直线的右上方作等边
,当动点
从点
运动到点
时,点
也随之运动,请直接写出点
运动路径的长.

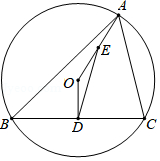
如图,已知锐角三角形内接于圆
,
于点
,连接
.
(1)若,
①求证:.
②当时,求
面积的最大值.
(2)点在线段
上,
,连接
,设
,
,
是正数),若
,求证:
.
如图,在平面直角坐标系中,抛物线与
轴交于点
,
(点
在点
的左侧),交
轴于点
,点
为抛物线的顶点,对称轴与
轴交于点
.
(1)连结,点
是线段
上一动点(点
不与端点
,
重合),过点
作
,交抛物线于点
(点
在对称轴的右侧),过点
作
轴,垂足为
,交
于点
,点
是线段
上一动点,当
取得最大值时,求
的最小值;
(2)在(1)中,当取得最大值,
取得最小值时,把点
向上平移
个单位得到点
,连结
,把
绕点
顺时针旋转一定的角度
,得到△
,其中边
交坐标轴于点
.在旋转过程中,是否存在一点
,使得
?若存在,请直接写出所有满足条件的点
的坐标;若不存在,请说明理由.

如图,是
的直径,
、
两点在
的延长线上,
是
上的点,且
,延长
至
,使得
,设
,
.
(1)求证:;
(2)求,
的长;
(3)若点在
、
、
三点确定的圆上,求
的长.

问题提出
(1)如图①,在中,
,
,点
关于
所在直线的对称点为
,则
的长度为 .
问题探究
(2)如图②,半圆的直径
,
是
的中点,点
在
上,且
,
是
上的动点,试求
的最小值.
问题解决
(3)如图③,扇形花坛的半径为
,
.根据工程需要.现想在
上选点
,在边
上选点
,在边
上选点
,用装饰灯带在花坛内的地面上围成一个
,使晚上点亮时,花坛中的花卉依然赏心悦目.为了既节省材料,又美观大方,需使得灯带
的长度最短,并且用长度最短的灯带围成的
为等腰三角形.试求
的值最小时的等腰
的面积.(安装损耗忽略不计)

在中,
,
分别是
两边的中点,如果
上的所有点都在
的内部或边上,则称
为
的中内弧.例如,图1中
是
的一条中内弧.

(1)如图2,在中,
,
,
分别是
,
的中点,画出
的最长的中内弧
,并直接写出此时
的长;
(2)在平面直角坐标系中,已知点,
,
,
,在
中,
,
分别是
,
的中点.
①若,求
的中内弧
所在圆的圆心
的纵坐标的取值范围;
②若在中存在一条中内弧
,使得
所在圆的圆心
在
的内部或边上,直接写出
的取值范围.
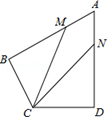
如图,在四边形ABCD中,AB=AD=6,AB⊥BC,AD⊥CD,∠BAD=60°,点M、N分别在AB、AD边上,若AM:MB=AN:ND=1:2.则∠BCD= °,cos∠MCN= .
若一个三角形的三个顶点均在一个图形的不同的边上,则称此三角形为该图形的内接三角形.
(1)在图①中画出△ABC的一个内接直角三角形;
(2)如图②,已知△ABC中,∠BAC=60°,∠B=45°,AB=8,AD为BC边上的高,探究以D为一个顶点作△ABC的内接三角形,其周长是否存在最小值?若存在,请求出最小值;若不存在,请说明理由;
(3)如图③,△ABC为等腰直角三角形,∠C=90°,AC=6,试探究:△ABC的内接等腰直角三角形的面积是否存在最小值?若存在,请求出最小值;若不存在,请说明理由.
先阅读短文,然后回答短文后面所给出的问题:
对于三个数a、b、c的平均数,最小的数都可以给出符号来表示,我们规定 表示这三个数的平均数,
表示这三个数的平均数,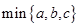 表示这三个数中的最小的数,
表示这三个数中的最小的数, 表示这三个数中最大的数.例如:
表示这三个数中最大的数.例如: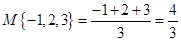 ,
,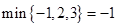 ,
,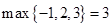 ;
; ,
, .
.
(1)请填空: ;若
;若 ,则
,则 ;
;
(2)若 ,求
,求 的取值范围;
的取值范围;
(3)若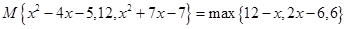 ,求
,求 的值.
的值.
某地因持续高温干旱,村民饮水困难,镇政府组织村民组成水源行动小组到村镇周边找水。某村民在山洞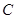 里发现了暗河(如图所示),经勘察,在山洞的西面有一条南北走向的公路连接着
里发现了暗河(如图所示),经勘察,在山洞的西面有一条南北走向的公路连接着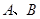 两村庄,山洞
两村庄,山洞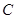 位于
位于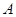 村庄南偏东
村庄南偏东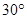 方向,且位于
方向,且位于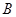 村庄南偏东
村庄南偏东 方向。为方便
方向。为方便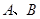 两村庄的村民取水,准备从山洞
两村庄的村民取水,准备从山洞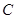 处向公路
处向公路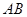 紧急修建一条最近的简易公路
紧急修建一条最近的简易公路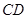 ,现已知
,现已知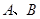 两村庄相距6千米。
两村庄相距6千米。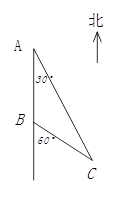
(1)求这条最近的简易公路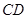 的长(精确到0.1千米)?
的长(精确到0.1千米)?
(2)现由甲、乙两施工队共同合作修建这条公路,已知甲施工队修建2千米后,由乙施工队继续修建,乙施工队每天施工的速度是甲施工队每天施工速度的1.6倍,8天后,公路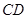 正式通车。求甲、乙两施工队每天修建公路多少千米?
正式通车。求甲、乙两施工队每天修建公路多少千米?
(参考数据: ,
,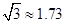 )
)
试题篮
()