初中数学频数（率）分布直方图试题

国家创新指数是反映一个国家科学技术和创新竞争力的综合指数．对国家创新指数得分排名前40的国家的有关数据进行收集、整理、描述和分析．下面给出了部分信息：

．国家创新指数得分的频数分布直方图（数据分成7组：，，，，，，；

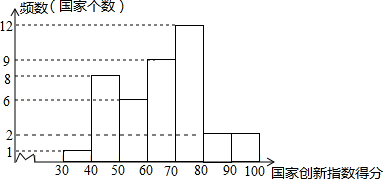
．国家创新指数得分在这一组的是：

61.7 62.4 63.6 65.9 66.4 68.5 69.1 69.3 69.5

．40个国家的人均国内生产总值和国家创新指数得分情况统计图：

．中国的国家创新指数得分为69.5．

（以上数据来源于《国家创新指数报告》

根据以上信息，回答下列问题：

（1）中国的国家创新指数得分排名世界第　　；

（2）在40个国家的人均国内生产总值和国家创新指数得分情况统计图中，包括中国在内的少数几个国家所对应的点位于虚线的上方，请在图中用“〇”圈出代表中国的点；

（3）在国家创新指数得分比中国高的国家中，人均国内生产总值的最小值约为　　万美元；（结果保留一位小数）

（4）下列推断合理的是　　．

①相比于点，所代表的国家，中国的国家创新指数得分还有一定差距，中国提出“加快建设创新型国家”的战略任务，进一步提高国家综合创新能力；

②相比于点，所代表的国家，中国的人均国内生产总值还有一定差距，中国提出“决胜全面建成小康社会”的奋斗目标，进一步提高人均国内生产总值．

某校共有200名学生，为了解本学期学生参加公益劳动的情况，收集了他们参加公益劳动时间（单位：小时）等数据，以下是根据数据绘制的统计图表的一部分

时间 $t$ 人数 学生类型		$0⩽t<10$	$10⩽t<20$	$20⩽t<30$	$30⩽t<40$	$t⩾40$
性别	男	7	31	25	30	4
	女	8	29	26	32	8
学段	初中		25	36	44	11
	高中

下面有四个推断：

①这200名学生参加公益劳动时间的平均数一定在 $24.5~25.5$ 之间

②这200名学生参加公益劳动时间的中位数在 $20~30$ 之间

③这200名学生中的初中生参加公益劳动时间的中位数一定在 $20~30$ 之间

④这200名学生中的高中生参加公益劳动时间的中位数可能在 $20~30$ 之间

所有合理推断的序号是 $($ 　　 $)$

A．

①③

B．

②④

C．

①②③

D．

①②③④

某年级共有300名学生．为了解该年级学生，两门课程的学习情况，从中随机抽取60名学生进行测试，获得了他们的成绩（百分制），并对数据（成绩）进行整理、描述和分析．下面给出了部分信息．

．课程成绩的频数分布直方图如下（数据分成6组：，，，，，

．课程成绩在这一组的是：70 71 71 71 76 76 77 78 78.5 78.5 79 79 79 79.5

．，两门课程成绩的平均数、中位数、众数如下：

课程	平均数	中位数	众数
	75.8		84.5
	72.2	70	83

根据以上信息，回答下列问题：

（1）写出表中的值；

（2）在此次测试中，某学生的课程成绩为76分，课程成绩为71分，这名学生成绩排名更靠前的课程是　　（填“”或“” ，理由是　　，

（3）假设该年级学生都参加此次测试，估计课程成绩超过75.8分的人数．

为了节约水资源，某市准备按照居民家庭年用水量实行阶梯水价．水价分档递增，计划使第一档、第二档和第三档的水价分别覆盖全市居民家庭的 $80\%$ ， $15\%$ 和 $5\%$ ，为合理确定各档之间的界限，随机抽查了该市5万户居民家庭上一年的年用水量（单位： $m^3)$ ，绘制了统计图．如图所示，下面四个推断合理的是 $($ 　　 $)$

①年用水量不超过 $180m^3$ 的该市居民家庭按第一档水价交费；

②年用水量超过 $240m^3$ 的该市居民家庭按第三档水价交费；

③该市居民家庭年用水量的中位数在 $150-180$ 之间；

④该市居民家庭年用水量的平均数不超过180．

A．

①③

B．

①④

C．

②③

D．

②④

为了解某校学生今年五一期间参加社团活动时间的情况，随机抽查了其中100名学生进行统计，并绘制成如图所示的频数直方图，已知该校共有1000名学生，据此估计，该校五一期间参加社团活动时间在 $8~10$ 小时之间的学生数大约是 $($ 　　 $)$

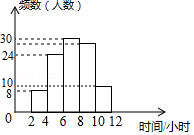
A．

280

B．

240

C．

300

D．

260

某学校认真开展学习和实践科学发展观活动，在阶段总结中提出对本单位今后的整改措施，并在征求教职工对整改方案的满意程度时进行民主测评，测评等级为：很满意、较满意、满意、不满意四个等级．
（1）若测评后结果如扇形图（图1），且测试等级为很满意、较满意、满意、不满意的人数之比为3：6：5：1，则图中α=         度，β=            度．
（2）若测试后部分统计结果如直方图（图2），请将直方图补画完整，并求出该单位职工总人数为人．
（3）按上级要求，满意度必须不少于95％方案才能通过，否则，必须对方案进行完善．若要使该方案完善后能获得通过，至少还需增加人对该方案的测评等级达满意（含满意）以上．

（年云南省昆明市）2015年4月25日，尼泊尔发生了里氏8．1级地震，某中学组织了献爱心捐款活动，该校教学兴趣小组对本校学生献爱心捐款额做了一次随机抽样调查，并绘制了不完整的频数分布表和频数分布直方图（每组含前一个边界值，不含后一个边界值）．如图所示：
     
（1）填空：a=        ，b=          ；
（2）补全频数分布直方图；
（3）该校共有1600名学生，估计这次活动中爱心捐款额不低于20元的学生有多少人？

（年贵州省铜仁市）为了增强学生的身体素质，教育部门规定学生每天参加体育锻炼时间不少于1小时，为了了解学生参加体育锻炼的情况，抽样调查了900名学生每天参加体育锻炼的时间，并将调查结果制成如下两幅不完整的统计图，请你根据图中提供的信息解答下列问题：

（1）请补充这次调查参加体育锻炼时间为1小时的频数分布直方图．
（2）求这次调查参加体育锻炼时间为1．5小时的人数．
（3）这次调查参加体育锻炼时间的中位数是多少？

（年新疆乌鲁木齐市）将九年级部分男生掷实心球的成绩进行整理，分成5个小组（x表示成绩，单位：米）．A组：5．25≤x＜6．25；B组：6．25≤x＜7．25；C组：7．25≤x＜8．25；D组：8．25≤x＜9．25；E组：9．25≤x＜10．25，并绘制出扇形统计图和频数分布直方图（不完整）．规定x≥6．25为合格，x≥9．25为优秀．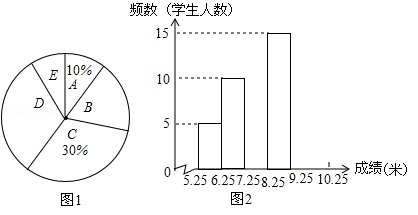

（1）这部分男生有多少人？其中成绩合格的有多少人？
（2）这部分男生成绩的中位数落在哪一组？扇形统计图中D组对应的圆心角是多少度？
（3）要从成绩优秀的学生中，随机选出2人介绍经验，已知甲、乙两位同学的成绩均为优秀，求他俩至少有1人被选中的概率．

（年云南省曲靖市）某企业为了解员工给灾区“爱心捐款”的情况，随机抽取部分员工的捐款金额整理绘制成如图所示的直方图，根据图中信息，下列结论正确的是（ ）

A．样本中位数是200元

B．样本容量是20

C．该企业员工捐款金额的极差是450元

D．该企业员工最大捐款金额是500元