初中数学条形统计图试题

为庆祝中国共产党建党100周年，某中学开展“学史明理、学史增信、学史崇德、学史力行”知识竞赛，现随机抽取部分学生的成绩分成 $A$、 $B$、 $C$、 $D$、 $E$五个等级进行统计，并绘制成两幅不完整的统计图，请根据图中提供的信息，解答下列问题：

（1）本次调查中共抽取 　　名学生；

（2）补全条形统计图；

（3）在扇形统计图中，求 $B$等级所对应的扇形圆心角的度数；

（4）若该校有1200名学生参加此次竞赛，估计这次竞赛成绩为 $A$和 $B$等级的学生共有多少名？

小明调查了本班每位同学最喜欢的颜色，并绘制了不完整的扇形图1及条形图2（柱的高度从高到低排列）．条形图不小心被撕了一块，图2中" $($ 　　 $)$ "应填的颜色是 $($ 　　 $)$

A．

蓝

B．

粉

C．

黄

D．

红

根据2021年5月11日国务院新闻办公室发布的《第七次全国人口普查公报》，就我国2020年每10万人中，拥有大学（指大专及以上）、高中（含中专）、初中、小学、其他等文化程度的人口（以上各种受教育程度的人包括各类学校的毕业生、肄业生和在校生）受教育情况数据，绘制了条形统计图（图 $1)$和扇形统计图（图 $2)$．

根据统计图提供的信息，解答下列问题：

（1） $a=$　　， $b=$　　；

（2）在第六次全国人口普查中，我国2010年每10万人中拥有大学文化程度的人数约为0.90万，则2020年每10万人中拥有大学文化程度的人数与2010年相比，增长率是 　　 $\%$（精确到 $0.1\%)$；

（3）2020年海南省总人口约1008万人，每10万人中拥有大学文化程度的人数比全国每10万人中拥有大学文化程度的人数约少0.16万，那么全省拥有大学文化程度的人数约有 　　万（精确到1万）．

2020年我国进行了第七次全国人口普查，小星要了解我省城镇及乡村人口变化情况，根据贵州省历次人口普查结果，绘制了如下的统计图表．请利用统计图表提供的信息回答下列问题：

贵州省历次人口普查城镇人口统计表

年份	1953	1961	1982	1990	2000	2010	2020
城镇人口（万人）	110	204	540	635	845	1175	2050
城镇化率	$7\%$	$12\%$	$19\%$	$20\%$	$24\%$	$a$	$53\%$

（1）这七次人口普查乡村人口数的中位数是 　　万人；

（2）城镇化率是一个国家或地区城镇人口占其总人口的百分率，是衡量城镇化水平的一个指标．根据统计图表提供的信息，我省2010年的城镇化率 $a$ 是 　　（结果精确到 $1\%)$ ；假设未来几年我省城乡总人口数与2020年相同，城镇化率要达到 $60\%$ ，则需从乡村迁入城镇的人口数量是 　　万人（结果保留整数）；

（3）根据贵州省历次人口普查统计图表，用一句话描述我省城镇化的趋势．

2021年是中国共产党建党100周年华诞．“五一”后某校组织了八年级学生参加建党100周年知识竞赛，为了了解学生对党史知识的掌握情况，学校随机抽取了部分同学的成绩作为样本，把成绩按不及格、合格、良好、优秀四个等级分别进行统计，并绘制了如下不完整的条形统计图与扇形统计图：

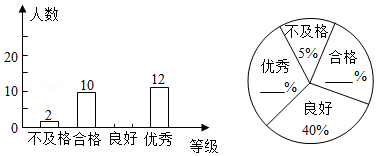
请根据图中提供的信息解答下列问题：

（1）根据给出的信息，将这两个统计图补充完整（不必写出计算过程）；

（2）该校八年级有学生650人，请估计成绩未达到“良好”及以上的有多少人？

（3）“优秀”学生中有甲、乙、丙、丁四位同学表现突出，现从中派2人参加区级比赛，求抽到甲、乙两人的概率．

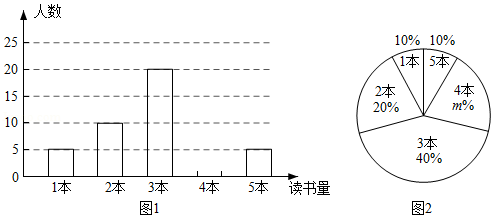
为迎接中国共产党建党100周年，某校开展了以“不忘初心，缅怀先烈”为主题的读书活动，学校政教处对本校七年级学生五月份“阅读该主题相关书籍的读书量”（下面简称“读书量” $)$进行了随机抽样调查，并对所有随机抽取学生的“读书量”（单位：本）进行了统计，如图所示：

（1）补全下面图1的统计图；

（2）本次所抽取学生五月份“读书量”的众数为 　　；

（3）已知该校七年级有1200名学生，请你估计该校七年级学生中，五月份“读书量”不少于4本的学生人数．

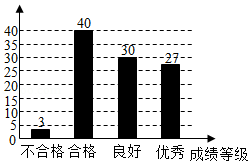
某中学九年级举办中华优秀传统文化知识竞赛．用简单随机抽样的方法，从该年级全体600名学生中抽取20名，其竞赛成绩如图：

（1）求这20名学生成绩的众数，中位数和平均数；

（2）若规定成绩大于或等于90分为优秀等级，试估计该年级获优秀等级的学生人数．

某校共有1000名学生．为了解学生的中长跑成绩分布情况，随机抽取100名学生的中长跑成绩，画出条形统计图，如图．根据所学的统计知识可估计该校中长跑成绩优秀的学生人数是 　   　．

每年的4月15日是我国全民国家安全教育日．某中学在全校七、八年级共800名学生中开展“国家安全法”知识竞赛，并从七、八年级学生中各抽取20名学生，统计这部分学生的竞赛成绩（竞赛成绩均为整数，满分10分，6分及以上为合格）．相关数据统计、整理如下：

八年级抽取的学生的竞赛成绩：

4，4，6，6，6，6，7，7，7，8，8，8，8，8，8，9，9，9，10，10．

七、八年级抽取的学生的竞赛成绩统计表

年级	七年级	八年级
平均数	7.4	7.4
中位数	a	b
众数	7	c
合格率	85%	90%

根据以上信息，解答下列问题：

（1）填空：a＝　　，b＝　　，c＝　　；

（2）估计该校七、八年级共800名学生中竞赛成绩达到9分及以上的人数；

（3）根据以上数据分析，从一个方面评价两个年级“国家安全法”知识竞赛的学生成绩谁更优异．

勤劳是中华民族的传统美德，学校要求学们在家帮助父母做一些力所能及的家务．在学期初，小丽同学随机调查了七年级部分同学寒假在家做家务的总时间，设被调查的每位同学寒假在家做家务的总时间为x小时，将做家务的总时间分为五个类别： $A（0\le x＜10）$， $B（10\le x＜20）$， $C（20\le x＜30）$， $D（30\le x＜40）$， $E（x\ge 40）$．并将调查结果绘制了如图两幅不完整的统计图：

根据统计图提供的作息，解答下列问题：

（1）本次共调查了　　名学生；

（2）根据以上信息直接在答题卡上补全条形统计图；

（3）扇形統计图中m＝　　，类别D所对应的扇形圆心角α的度数是　　度；

（4）若该校七年级共有400名学生，根据抽样调查的结果，估计该校七年級有多少名学生寒假在家做家务的总时间不低于20小时？

为培养学生正确的劳动价值观和良好劳动品质，加强新时代中学生劳动教育，某校八年级（1）班对本班35名学生进行了劳动能力量化评估和近一周家务劳动总时间调查，并对相关数据进行了收集、整理和分析，研究过程中的部分数据如下：

信息一：劳动能力量化评估的成绩采用十分制，得分均为整数；

信息二：

信息三：

近一周家务劳动时间分布表

时间/小时	$t\le 1$	$1＜t\le 2$	$2＜t\le 3$	$3＜t\le 4$	$t＞4$
人数/人	5	8	12	7	3

信息四：

劳动能力量化成绩与近一周家务劳动总时间统计表

成绩/分 人数 时间/小时	6	7	8	9	10
$t\le 1$	4	1	0	0	0
$1＜t\le 2$	0	6	1	1	0
$2＜t\le 3$	0	0	9	3	0
$3＜t\le 4$	0	1	1	3	2
$t＞4$	0	0	0	1	2

根据以上信息，解决下列问题：

（1）直接从信息二的统计图中“读”出八年级（1）班劳动能力量化成绩的平均分为　　分；

（2）请你判断下列说法合理吗？（请在横线上填写“合理”或“不合理”）

①规定劳动能力量化成绩8分及以上为合格，八年级（1）班超过半数的学生达到了合格要求：　　．

②班主任对近一周家务劳动总时间在4小时以上，且劳动能力量化成绩取得10分的学生进行表彰奖励，恰有3人获奖：　　．

③小颖推断劳动能力量化成绩为8分的同学近一周家务劳动总时间主要分布在 $2＜t\le 3$的时间段：　　．

（3）结合以上信息，你认为普遍情况下参加家务劳动的时间与劳动能力之间具有怎样的关系？

某校数学实践小组就近期人们比较关注的五个话题：“ $A$． $5G$通讯； $B$．民法典； $C$．北斗导航； $D$．数字经济； $E$．小康社会”，对某小区居民进行了随机抽样调查，每人只能从中选择一个本人最关注的话题，根据调查结果绘制了如图两幅不完整的统计图．

请结合统计图中的信息，解决下列问题：

（1）数学实践小组在这次活动中，调查的居民共有　 　人；

（2）将上面的最关注话题条形统计图补充完整；

（3）最关注话题扇形统计图中的 $a=$　　，话题 $D$所在扇形的圆心角是　　度；

（4）假设这个小区居民共有10000人，请估计该小区居民中最关注的话题是“民法典”的人数大约有多少？

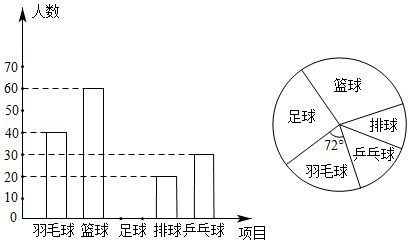
奥体中心为满足暑期学生对运动的需求，欲开设球类课程，该中心随机抽取部分学生进行问卷调查，被调查学生须从“羽毛球”、“篮球”、“足球”、“排球”、“乒乓球”中选择自己最喜欢的一项．根据调查结果绘制了不完整的条形统计图和扇形统计图，请根据图中信息，解答下列问题：

（1）此次共调查了多少名学生？

（2）将条形统计图补充完整；

（3）我们把“羽毛球”“篮球”，“足球”、“排球”、“乒乓球”分别用 $A$， $B$， $C$， $D$， $E$表示．小明和小亮分别从这些项目中任选一项进行训练，利用树状图或表格求出他俩选择不同项目的概率．

为了调查疫情对青少年人生观、价值观产生的影响，某学校团委对初二级部学生进行了问卷调查，其中一项是：疫情期间出现的哪一个高频词汇最触动你的内心？针对该项调查结果制作的两个统计图（不完整）如图．由图中信息可知，下列结论错误的是 $($　　 $)$

A．本次调查的样本容量是600

B．选“责任”的有120人

C．扇形统计图中“生命”所对应的扇形圆心角度数为 $64.8°$

D．选“感恩”的人数最多

为迎接2020年第35届全国青少年科技创新大赛，某学校举办了 $A$ ：机器人； $B$ ：航模； $C$ ：科幻绘画； $D$ ：信息学； $E$ ：科技小制作等五项比赛活动（每人限报一项），将各项比赛的参加人数绘制成如图两幅不完整的统计图．

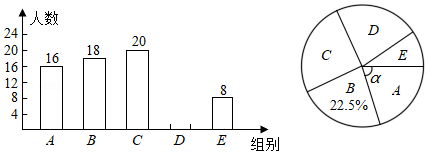
根据统计图中的信息解答下列问题：

（1）本次参加比赛的学生人数是 　 　名；

（2）把条形统计图补充完整；

（3）求扇形统计图中表示机器人的扇形圆心角 $\alpha$ 的度数；

（4）在 $C$ 组最优秀的3名同学 $(1$ 名男生2名女生）和 $E$ 组最优秀的3名同学 $(2$ 名男生1名女生）中，各选1名同学参加上一级比赛，利用树状图或表格，求所选两名同学中恰好是1名男生1名女生的概率．