初中数学列表法与树状图法试题

为了弘扬爱国主义精神，某校组织了"共和国成就"知识竞赛，将成绩分为： $A$ （优秀）、 $B$ （良好）、 $C$ （合格）、 $D$ （不合格）四个等级．小李随机调查了部分同学的竞赛成绩，绘制了如图统计图．

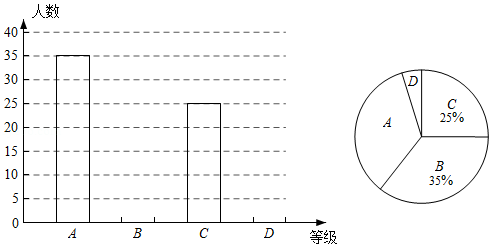
（1）本次抽样调查的样本容量是 　　，请补全条形统计图；

（2）已知调查对象中只有两位女生竞赛成绩不合格，小李准备随机回访两位竞赛成绩不合格的同学，请用树状图或列表法求出恰好回访到一男一女的概率；

（3）该校共有2000名学生，请你估计该校竞赛成绩"优秀"的学生人数．

如图所示的转盘，被分成面积相等的四个扇形，分别涂有红、黄、蓝、绿四种颜色．固定指针，自由转动转盘两次，每次停止后，记下指针所指区域（指针指向区域分界线时，忽略不计）的颜色，则两次颜色相同的概率是　　．

今年某市为创评“全国文明城市”称号，周末团市委组织志愿者进行宣传活动．班主任梁老师决定从4名女班干部（小悦、小惠、小艳和小倩）中通过抽签方式确定2名女生去参加．抽签规则：将4名女班干部姓名分别写在4张完全相同的卡片正面，把四张卡片背面朝上，洗匀后放在桌面上，梁老师先从中随机抽取一张卡片，记下姓名，再从剩余的3张卡片中随机抽取第二张，记下姓名．

（1）该班男生“小刚被抽中”是　　事件，“小悦被抽中”是　　事件（填“不可能”或“必然”或“随机” $)$；第一次抽取卡片“小悦被抽中”的概率为　　；

（2）试用画树状图或列表的方法表示这次抽签所有可能的结果，并求出“小惠被抽中”的概率．

现有四张正面分别标有数字 $-1$，1，2，3的不透明卡片，它们除数字外其余完全相同，将它们背面朝上洗均匀，随机抽取一张，记下数字后放回，背面朝上洗均匀，再随机抽取一张记下数字，前后两次抽取的数字分别记为 $m$， $n$．则点 $P(m,n)$在第二象限的概率为　　．

现有4盒同一品牌的牛奶，其中2盒已过期，随机抽取2盒，至少有一盒过期的概率是 $($ 　　 $)$

A．

$\frac{1}{2}$

B．

$\frac{2}{3}$

C．

$\frac{3}{4}$

D．

$\frac{5}{6}$

甲、乙两个家庭来到以“生态资源，绿色旅游”为产业的美丽云南，各自随机选择到大理、丽江、西双版纳三个城市中的一个城市旅游．假设这两个家庭选择到哪个城市旅游不受任何因素影响，上述三个城市中的每一个被选到的可能性相同，甲、乙两个家庭选择到上述三个城市中的同一个城市旅游的概率为 $P$．

（1）直接写出甲家庭选择到大理旅游的概率；

（2）用列表法或树状图法（树状图也称树形图）中的一种方法，求 $P$的值．

一个不透明的口袋中有三个完全相同的小球，它们的标号分别为1，2，3．随机摸出一个小球然后放回，再随机摸出一个小球，则两次摸出的小球标号相同的概率是　　．

某校组织开展运动会，小明和扎西两名同学准备从100米短跑（记为项目 $A)$，800米中长跑（记为项目 $B)$，跳远（记为项目 $C)$，跳高（记为项目 $D)$，即从 $A$， $B$， $C$， $D$四个项目中，分别选择一个项目参加比赛．请用画树状图或列表法求两名同学选到相同项目的概率．

箱子里放有2个黑球和2个红球，它们除颜色外其余都相同，现从箱子里随机摸出两个球，恰好为1个黑球和1个红球的概率是　　．

箱子里放有2个黑球和2个红球，它们除颜色外其余都相同，现从箱子里随机摸出两个球，恰好为1个黑球和1个红球的概率是　　．

某居委会组织两个检查组，分别对“垃圾分类”和“违规停车”的情况进行抽查．各组随机抽取辖区内某三个小区中的一个进行检查，则两个组恰好抽到同一个小区的概率是 $($　　 $)$

A． $\frac{1}{9}$B． $\frac{1}{6}$C． $\frac{1}{3}$D． $\frac{2}{3}$

一只不透明袋子中装有三只大小、质地都相同的小球，球面上分别标有数字1、 $-2$、3，搅匀后先从中任意摸出一个小球（不放回），记下数字作为点 $A$的横坐标，再从余下的两个小球中任意摸出一个小球，记下数字作为点 $A$的纵坐标．

（1）用画树状图或列表等方法列出所有可能出现的结果；

（2）求点 $A$落在第四象限的概率．

每年6月26日是“国际禁毒日”．某中学为了让学生掌握禁毒知识，提高防毒意识，组织全校学生参加了“禁毒知识网络答题”活动．该校德育处对八年级全体学生答题成绩进行统计，将成绩分为四个等级：优秀、良好、一般、不合格；并绘制成如图不完整的统计图．请你根据图1．图2中所给的信息解答下列问题：

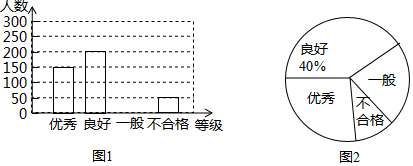
（1）该校八年级共有　 　名学生，“优秀”所占圆心角的度数为　　．

（2）请将图1中的条形统计图补充完整．

（3）已知该市共有15000名学生参加了这次“禁毒知识网络答题”活动，请以该校八年级学生答题成绩统计情况估计该市大约有多少名学生在这次答题中成绩不合格？

（4）德育处从该校八年级答题成绩前四名甲，乙、丙、丁学生中随机抽取2名同学参加全市现场禁毒知识竞赛，请用树状图或列表法求出必有甲同学参加的概率．

如图在三条横线和三条竖线组成的图形中，任选两条横线和两条竖线都可以围成一个矩形，从这些矩形中任选一个，则所选矩形含点 $A$ 的概率是 $($ 　　 $)$

A．

$\frac{1}{4}$

B．

$\frac{1}{3}$

C．

$\frac{3}{8}$

D．

$\frac{4}{9}$

为了倡导“节约用水，从我做起”，某市政府决定对该市直属机关200户家庭用水情况进行调查．市政府调查小组随机抽查了其中部分家庭一年的月平均用水量（单位：吨），调查中发现，每户家庭月平均用水量在 $3~7$吨范围内，并将调查结果制成了如下尚不完整的统计表：

月平均用水量（吨 $)$	3	4	5	6	7
频数（户数）	4	$a$	9	10	7
频率	0.08	0.40	$b$	$c$	0.14

请根据统计表中提供的信息解答下列问题：

（1）填空： $a=$　　， $b=$　　， $c=$　　．

（2）这些家庭中月平均用水量数据的平均数是 　　，众数是 　　，中位数是 　　．

（3）根据样本数据，估计该市直属机关200户家庭中月平均用水量不超过5吨的约有多少户？

（4）市政府决定从月平均用水量最省的甲、乙、丙、丁四户家庭中，选取两户进行“节水”经验分享．请用列表或画树状图的方法，求出恰好选到甲、丙两户的概率，并列出所有等可能的结果．