初中数学对称式和轮换对称式选择题

如图，△ABC的三个顶点都在方格纸的格点上，其中点A的坐标是（﹣1，0）．现将△ABC绕点A顺时针旋转90°，则旋转后点C的坐标是

A．（2，1）

B．（1，2）

C．（-2，-1）

D．（-2，1）

如图，P是等边△ABC内的一点，若将△PAB绕点A逆时针旋转得到△P’AC，则∠PAP’的度数为

A．120°

B．90°

C．60°

D．30°

如图，小明使一长为4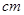，宽为3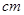的长方形木板，在桌面上做无滑动的翻滚（顺时针方向）木板上点A位置变化为，其中第二次翻滚被桌面上一小木块挡住，使木板与桌面成30°角，则点A翻滚到A₂位置时共走过的路径长为（）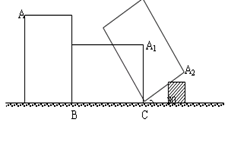

A．10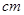

B．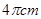

C．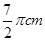

D．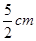

在平面直角坐标系中，P点关于原点的对称点为P₁（-3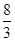，-），P点关于x轴的对称点为P₂（a，b），则=（）

A．-2

B．2

C．4

D．-4

平面直角坐标系中，O为坐标原点，点A的坐标为（，1），将OA绕原点按逆时针方向旋转90°得OB，则点B的坐标为（）

A．（1，）

B．（ －1，）

C．（0，2）

D．（2，0）

长方形ABCD中，AD="4" cm，AB="10" cm，按右图方式折叠，使点B与点D重合，折痕是EF，则DE等于（）

A．4．2 cm

B．5．8 cm

C．4．2 cm或5．8 cm

D．6 cm

如图，坐标平面内一点A（2，-1），O为原点，P是x轴上的一个动点，如果以点P、O、A为顶点的三角形是等腰三角形，那么符合条件的动点P的个数为（）

A．2

B．3

C．4

D．5

下列电视台的台标，是中心对称图形的是（）

A．

B．

C．

D．

下面四个图形分别是节能、节水、绿色食品和低碳标志，在这四个标志中，是轴对称图形的是（）

A．

B．

C．

D．

观察下列图形，是中心对称图形的是（）

如图，点P是∠AOB外的一点，点M，N分别是∠AOB两边上的点，点P关于OA的对称点Q恰好落在线段MN上，点P关于OB的对称点R落在MN的延长线上．若PM=3cm，PN=4cm，MN=4.5cm，则线段QR的长为（）

A．4.5

B．5.5

C．6.5

D．7

已知等腰三角形一边长为4，一边的长为10，则等腰三角形的周长为（）

A．14

B．18

C．24

D．18或24

下列图形中，对称轴最多的是（）

A．等腰三角形	B．等边三角形
C．直角三角形	D．等腰直角三角形

如图，有a、b、c三户家用电路接入电表，相邻电路的电线等距排列，则三户所用电线（）

A．a户最长

B．b户最长

C．c户最长

D．三户一样长

将一张正方形纸片按如图1、图2所示的方向对折，然后沿图3中的虚线剪裁得到图4，将图4的纸片展开铺平，得到的图案是（）