王老师给学生分作业本,若每人分4本,则多8本,若每人分5本,则少2本,则学生数、本数分别为( )
| A.18人,40本 | B.10人,48本 | C.50人,8本 | D.18人,5本 |
小明和小刚从相距25.2千米的两地同时相向而行,小明每小时走4千米,3小时后两人相遇,设小刚的速度为 千米/时,列方程得( )
千米/时,列方程得( )
A. |
B. |
C. |
D. |
甲、乙两地同时生产某种蔬菜若干吨,现甲地可外销这种蔬菜10吨,乙地可外销这种蔬菜4吨,经调查A、B两城各需这种蔬菜分别为8吨和6吨.每吨这种蔬菜的运费如下表.设乙地运往B城的这种蔬菜为x吨.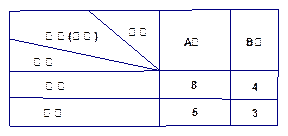
(1)用含x的代数式来表示总运费(单位:百元/吨);
(2)若总运费为8400元,则乙地运往A城的这种蔬菜为多少吨?
(3)试问有无可能总运费为7400元?若有可能,请写出相应的调动方案;若无可能,请说明理由.
(6分) 某自行车厂一周计划生产1400辆自行车,平均每天生产自行车200辆,由于各种原因,实际每天生产量与计划每天生产量相比有出入。下表是某周的自行车生产情况(超计划生产量为正、不足计划生产量为负,单位:辆):
| 星期 |
一 |
二 |
三 |
四 |
五 |
六 |
日 |
| 增减 |
+5 |
-2 |
-4 |
+13 |
-10 |
+16 |
-9 |
(1)根据记录可知前三天共生产自行车________辆;
(2)产量最多的一天比产量最少的一天多生产________辆;
(3)若该厂实行按生产的自行车数量的多少计工资,即计件工资制。如果每生产一辆自行车可得人民币60 元,那么该厂工人这一周的工资总额是多少元?
某学生从家到学校时,每小时行5千米;按原路返回家时,每小时行4千米 ,结果返回的时间比去学校的时间多花10分钟.设去学校所用时间为 小时,则可列方程得 ( )
小时,则可列方程得 ( )
A. |
B. |
C. |
D. |
如图是某月的月历.
(1)图中带阴影的方框中的9个数之和与方框正中心的数有什么关系?请说明你的理由?
(2)若这9个数之和是81,你能说出这9个日期吗?只要回答能或不能,且说明为什么?
(3)这9个数之和可能会是100吗?如果可能,请计算出这9个日期,如果不可能,请说明为什么?
解方程:
x﹣
解:去分母,得6x﹣3x+1=4﹣2x+4…①
即﹣3x+1=﹣2x+8…②
移项,得﹣3x+2x=8﹣1…③
合并同类项,得﹣x=7…④
∴x=﹣7…⑤
上述解方程的过程中,是否有错误?答: 有 ;如果有错误,则错在 ① 步.如果上述解方程有错误,请你给出正确的解题过程.
(本题8分)“湖田十月清霜堕,晚稻初香蟹如虎”,又到了食蟹的好季节啦!某经销商去水产批发市场采购太湖蟹,他看中了A、B两家的某种品质相近的太湖蟹.零售价都为60元/千克,批发价各不相同.
A家规定:批发数量不超过100千克,按零售价的9 2%优惠;批发数量超过100千克但不超过200千克,按零售价的90%优惠;超过200千克的按零售价的88%优惠.
2%优惠;批发数量超过100千克但不超过200千克,按零售价的90%优惠;超过200千克的按零售价的88%优惠.
B家的规定如下表:
| 数量范围(千克) |
0~50 部分 |
50以上~150 部分 |
150以上~250 部分 |
250以上 部分 |
| 价 格(元) |
零售价的95% |
零售价的85% |
零售价的75% |
零售价的70% |
(1)如果他批发80千克太湖蟹,则他在A 、B两家批发分别需要多少元?
(2)如果他批发x千克太湖蟹 (150<x<200),请你分别用含字母x的式子表示他在A 、B两家批发所需的费用;
(3)现在他要批发195千克太湖蟹,你能帮助他选择在哪家批发更优惠吗?请说明理由.
“家电下乡”农民得实惠,村民小郑购买一台双门冰箱,在扣除13%的政府财政补贴后,再减去商场赠送的“家电下乡”消费券100元,实际只花了1648.7元,那么他购买这台冰箱节省了__________元钱;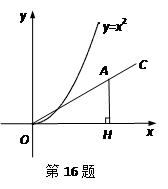
(6分)七年级一班共有48名同学,班级决定每人购买一本定价为5元的《中学生数学学习手册》,书店对购买50本及50本以上者给予九折优惠,请你设计一下,怎样买书最省钱?
(9分)某商店打出了促销广告如下表.对顾客实行优惠,某人在此商场两次购物分别付款168元和423元.(1)第一次付款168元,可购价值多少元的货物?(2)第二次付款423元,可购价值多少元的货物?(3)若把两次的货物合在一次买,需要多少钱?
| 优惠条件 |
一次购物不超过200元 |
一次购物超过200元,但不超过500元 |
一次购物超过500元 |
| 优惠方法 |
不予优惠 |
按物价给予九折优惠 |
其中500元按九折优惠,超过500元部分按八折优惠. |
试题篮
()