初中数学应用类问题试题

为了参加2011年国际铁人三项（游泳、自行车、长跑）系列赛业余组的比赛，李明针对自行车和长跑项目进行专项训练．某次训练中，李明骑自行车的平均速度为每分钟600米，跑步的平均速度为每分钟200米，自行车路段和长跑路段共5千米，用时15分钟．求自行车路段和长跑路段的长度．

解方程：
解方程组：

如图，用围棋子按下面的规律摆图形，则摆第n个图形需要围棋子的枚数为（    ）

A．5n	B．5n－1
C．6n－1	D．2n^2＋1

某书店老板去图书批发市场购买某种图书．第一次用1200元购书若干本，并按该书定价7元出售，很快售完．由于该书畅销，第二次购书时，每本书的批发价已比第一次提高了20%，他用1500元所购该书数量比第一次多10本．当按定价售出200本时，出现滞销，便以定价的4折售完剩余的书．试问该老板这两次售书总体上是赔钱了，还是赚钱了（不考虑其它因素）？若赔钱，赔多少？若赚钱，赚多少？

在密码学中，直接可以看到的内容为明码，对明码进行某种处理后得到的内容为密码。有一种密码，将英文的26个字母a,b,c……z（不论大小写）依次对应1,2,3……26这26个自然数（见表格）。当明码对应的序号x为奇数时，密码对应的序号；当明码对应的序号x为偶数时，密码对应的序号为。

字母	a	b	c	d	e	f	g	h	i	j	k	l	m
序号	1	2	3	4	5	6	7	8	9	10	11	12	13
字母	n	o	p	q	r	s	t	u	v	w	x	y	z
序号	14	15	16	17	18	19	20	21	22	23	24	25	26

按上述规定，将明码“love”译成的密码是（   ）
A．gawq           B．shxc          C．sdri            D．love  

铜仁某水果店销售公司准备从外地购买西瓜31吨、柚子12吨，现计划租甲、乙两种货车共10辆，将这批水果运到铜仁，已知甲种货车可装西瓜4吨和柚子1吨，乙种货车可装西瓜、柚子2吨
该公司安排甲、乙两种货车时有几种方案？
若甲种货车每辆要付运输费用1800元，乙种货车每辆要付运输费用1200元，则该公司选择哪种方案运费最少？最少运费是多少？

如图12，端午节期间，某地举行龙舟比赛。甲、乙两支龙舟队在比赛时路程y（米）与时间x（分钟）之间的函数图象如图所示，根据图象回答下列问题：

1.8分时，哪支龙舟队处于领先位置？
在这次龙舟比赛中，哪只龙舟队先到达终点？先到达多长时间？
求乙队加速后，路程y（米）与时间x（分钟）之间的函数解析式。

一组数1，, ,2 ,…符合这个规律的第8个数是     。

病人按规定的剂量服用某种药物．测得服药后2小时，每毫升血液中的含药量达到最大值为4毫克．已知服药后，2小时前每毫升血液中的含药量y（毫克）与时间x（小时）成正比例；2小时后y与x成反比例（如图所示）．根据以上信息解答下列问题：

求当0≤x≤2时，y与x的函数关系式
求当x>2时，y与x的函数关系式
若每毫升血液中的含药量不低于2毫克时治疗有效，则服药一次，治疗疾病的有效时间是多长？

从美学角度来说，人的上身长与下身长之比为黄金比时，可以给人一种协调的美感，某女老师上身长约61.80cm，下身长约93.00cm，她要穿约_______cm的高跟鞋才能达到黄金比的美感效果(精确到0.01cm)．

某电器城经销A型号彩电，2011年四月份每台彩电售价为2 000元，与去年同期相比，结果卖出彩电的数量相同，但去年销售额为5万元，今年销售额只有4万元．
2010年四月份每台A型号彩电的售价是多少元？
为了改善经营，电器城决定再经销B型号彩电，已知A型号彩电每台进货价为1 800元，B型号彩电每台进货价为1500元，电器城预计用不大于3.3万元且不少于3.2万元的资金购进这两种彩电共20台，有哪几种进货方案？
电器城准备把A型号彩电继续以原价每台2000元的价格出售，B型号彩电以每台1800元的价格出售，在这批彩电全部卖出的前提下，如何进货才能使电器城获利最大？最大利润是多少？

同学们，我们曾经研究过n×n的正方形网格，得到了网格中正方形的总数的表达式为．但n为100时，应如何计算正方形的具体个数呢？下面我们就一起来探究并解决这个问题．首先，通过探究我们已经知道时，我们可以这样做：
观察并猜想：
=（1+0）×1+（1+1）×2=l+0×1+2+1×2=（1+2）+（0×1+1×2）
=（1+0）×1+（1+1）×2+（l+2）×3
=1+0×1+2+1×2+3+2×3
=（1+2+3）+（0×1+1×2+2×3）
=（1+0）×1+（1+1）×2+（l+2）×3+（1+3）×4；
=1+0×1+2+1×2+3+2×3+（ ___________）
=（1+2+3+4）+（___________）
…
归纳结论：
=（1+0）×1+（1+1）×2+（1+2）×3+…[（1+（n-l）]n
=1+0×1+2+1×2+3+2×3+…+n+（n-1）×n
=（___________）+[ ___________]
= （__________）+（ ___________）
=×(___________)
实践应用：
通过以上探究过程，我们就可以算出当n为100时，正方形网格中正方形的总个数是___。

如图所示，圆圈内分别标有1，2，…，12，这12个数字，电子跳蚤每跳一步，可以从一个圆圈逆时针跳到相邻的圆圈，若电子跳蚤所在圆圈的数字为，则电子跳蚤连续跳（）步作为一次跳跃，例如：电子跳蚤从标有数字1的圆圈需跳步到标有数字2的圆圈内，完成一次跳跃，第二次则要连续跳步到达标有数字6的圆圈，…依此规律，若电子跳蚤从①开始，那么第3次能跳到的圆圈内所标的数字为     ；第2012次电子跳蚤能跳到的圆圈内所标的数字为      ．

如图，在平面直角坐标系中，点A，B的坐标分别为A（2，4），B（4，0）.
以原点O为位似中心，把线段AB缩小为原来的；
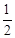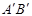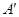若（1）中画出的线段为，请写出线段两个端点,的坐标；
若线段AB上任意一点M的坐标为（a，b），请写出缩小后的线段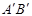上对应点
的坐标．
                                   

如图，在△ABC中，AB=AC．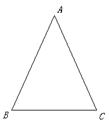

作∠BAC的角平分线，交BC于点D（尺规作图，保留痕迹）；
在AD的延长线上任取一点E，连接BE、CE． 求证：△BDE≌△CDE；
当AE=2AD时，四边形ABEC是菱形．请说明理由．