初中数学应用类问题试题

从美学角度来说，人的上身长与下身长之比为黄金比时，可以给人一种协调的美感，某女老师上身长约61.80cm，下身长约93.00cm，她要穿约_______cm的高跟鞋才能达到黄金比的美感效果(精确到0.01cm)．

观察数表

根据表中数的排列规律，则B+D=　   　．

某电器城经销A型号彩电，2011年四月份每台彩电售价为2 000元，与去年同期相比，结果卖出彩电的数量相同，但去年销售额为5万元，今年销售额只有4万元．
2010年四月份每台A型号彩电的售价是多少元？
为了改善经营，电器城决定再经销B型号彩电，已知A型号彩电每台进货价为1 800元，B型号彩电每台进货价为1500元，电器城预计用不大于3.3万元且不少于3.2万元的资金购进这两种彩电共20台，有哪几种进货方案？
电器城准备把A型号彩电继续以原价每台2000元的价格出售，B型号彩电以每台1800元的价格出售，在这批彩电全部卖出的前提下，如何进货才能使电器城获利最大？最大利润是多少？

同学们，我们曾经研究过n×n的正方形网格，得到了网格中正方形的总数的表达式为．但n为100时，应如何计算正方形的具体个数呢？下面我们就一起来探究并解决这个问题．首先，通过探究我们已经知道时，我们可以这样做：
观察并猜想：
=（1+0）×1+（1+1）×2=l+0×1+2+1×2=（1+2）+（0×1+1×2）
=（1+0）×1+（1+1）×2+（l+2）×3
=1+0×1+2+1×2+3+2×3
=（1+2+3）+（0×1+1×2+2×3）
=（1+0）×1+（1+1）×2+（l+2）×3+（1+3）×4；
=1+0×1+2+1×2+3+2×3+（ ___________）
=（1+2+3+4）+（___________）
…
归纳结论：
=（1+0）×1+（1+1）×2+（1+2）×3+…[（1+（n-l）]n
=1+0×1+2+1×2+3+2×3+…+n+（n-1）×n
=（___________）+[ ___________]
= （__________）+（ ___________）
=×(___________)
实践应用：
通过以上探究过程，我们就可以算出当n为100时，正方形网格中正方形的总个数是___。

一些较大数值问题可以通过用字母代替数成整式问题来解决，请先阅读下面的解题过程，再解答后面的问题．
例： 若x=123456789×123456786，
y=123456788×123456787，
试比较x、y的大小．
解： 设123456788=a，
那么x=， y=
∵
∴x＜y
看完后，你学到了这种方法吗？再亲自试一试吧，你准行！

(1)若x=234567×234568，y=234566×234569，比较比较x、y的大小
(2)计算：

下图是在正方形网格中按规律填成的阴影，根据此规律，则第n个图中阴影部
分小正方形的个数是       ．

如图所示，圆圈内分别标有1，2，…，12，这12个数字，电子跳蚤每跳一步，可以从一个圆圈逆时针跳到相邻的圆圈，若电子跳蚤所在圆圈的数字为，则电子跳蚤连续跳（）步作为一次跳跃，例如：电子跳蚤从标有数字1的圆圈需跳步到标有数字2的圆圈内，完成一次跳跃，第二次则要连续跳步到达标有数字6的圆圈，…依此规律，若电子跳蚤从①开始，那么第3次能跳到的圆圈内所标的数字为     ；第2012次电子跳蚤能跳到的圆圈内所标的数字为      ．

如下表，从左到右在每个小格子中都填入一个整数，使得其中任意三个相邻格子中 所填整数之和都相等，则第2012个格子中的数为（　　）

3

a

b

c

﹣1

2

…

 
A.3     B.2      C.0        D.﹣1

对于每个非零自然数n，抛物线与x轴交于A_n、B_n两点，以表示这两点间的距离，则的值是（      ）

A．

B．

C．

D．

某运输部门规定：办理托运，当一种物品的重量不超过16千克时，需付基础费30元和保险费a元：为限制过重物品的托运，当一件物品超过16千克时，除了付以上基础费和保险费外，超过部分每千克还需付b元超重费。设某件物品的重量为x千克。
(1)当x≤16时，支付费用为__________________元(用含a的代数式表示)；
当x≥16时，支付费用为_________________元(用含x和a、b的代数式表示)；
(2)甲、乙两人各托运一件物品，物品重量和支付费用如下表所示

物品重量（千克）	支付费用（元）
18	39
25	53

试根据以上提供的信息确定a，b的值。
（3）根据这个规定，若丙要托运一件超过16千克的物品，但支付的费用不想超过70元，那么丙托运的物品最多是多少千克？

如图，在平面直角坐标系中，点A，B的坐标分别为A（2，4），B（4，0）.
以原点O为位似中心，把线段AB缩小为原来的；
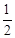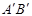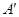若（1）中画出的线段为，请写出线段两个端点,的坐标；
若线段AB上任意一点M的坐标为（a，b），请写出缩小后的线段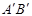上对应点
的坐标．
                                   

如图,已知：在边长为12的正方形ABCD中,有一个小正方形EFGH,其中E、F、G分别在AB、BC、FD上.若BF＝3,则BE长为（ ）

A．1                B．2.5              C．2.25             D．1.5

从边长为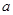的大正方形纸板中挖去一个边长为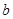的小正方形纸板后，将其裁成四个相同的等腰梯形（图甲），然后拼成一个平行四边形（图乙）．那么通过计算两个图形阴影部分的面积，可以验证成立的公式是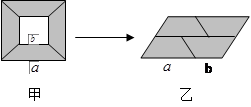

如图，在△ABC中，AB=AC．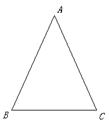

作∠BAC的角平分线，交BC于点D（尺规作图，保留痕迹）；
在AD的延长线上任取一点E，连接BE、CE． 求证：△BDE≌△CDE；
当AE=2AD时，四边形ABEC是菱形．请说明理由．

先阅读下列材料，再解答后面的问题
材料：一般地，n个相同的因数相乘：。如2³=8，此时，3叫做以2为底8的对数，记为。一般地，若，则n叫做以为底b的对数，记为，则4叫做以3为底81的对数，记为。
问题：
计算以下各对数的值：log₂4=           log₂16=         log₂64=        
观察(1)中三数4、16、64之间满足怎样的关系式？log₂4、log₂16、log₂64之间又满足怎样的关系式？
由(2)的结果，你能归纳出一个一般性的结论吗？      log_aM+log_aN=         (a>0且a≠1，M>0，N>0)
根据幂的运算法则：aⁿ·a^m=a^n+m以及对数的含义证明上述结论