初中数学三角形的五心试题

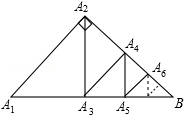
如图，△A₁A₂B是直角三角形，∠A₁A₂B=90⁰，且A₁A₂＝A₂B＝4， A₂A₃⊥A₁B，垂足为A₃，A₃A₄⊥A₂B，垂足为A₄，A₄A₅⊥A₃B，垂足为A₅，A₅A₆⊥A₄B，垂足为A₆，一直按此做去，……则△A_nA_n+1B的面积为                    ．

（1）如图1，已知△ABC，以AB、AC为边向△ABC外作等边△ABD和等边△ACE，连接BE，CD，请你完成图形（尺规作图，保留作图痕迹），并猜想BE与CD的关系：___________；你是通过证明_______________ 得到的；
（2）如图2，已知△ABC，以AB、AC为边向外作正方形ABFD和正方形ACGE，连接BE，CD，BE与CD有什么数量关系？并说明理由；
（3）运用（1）、（2）解答中所积累的经验和知识，完成下题：
如图3，要测量池塘两岸相对的两点B，E的距离，已经测得∠ABC=45°，∠CAE=90°，AB=BC=100米，AC=AE，求BE的长．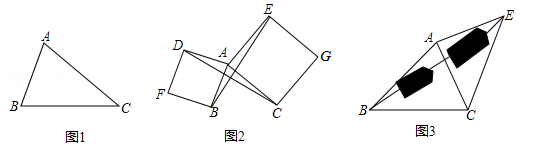

如图，△ABC面积为1，第一次操作：分别延长AB，BC，CA至点A₁，B₁， C₁，使A₁B=AB、B₁C=2BC，C₁A=2CA，顺次连接A₁，B₁，C₁，得到△A₁B₁C₁．第二次操作：分别延长A₁B₁，B₁C₁、C₁A₁至点A₂，B₂，C₂，使A₂B₁=A₁B₁，B₂C₁=2B₁C₁，C₂A₁=2C₁A₁，顺次连接A₂，B₂，C₂，得到△A₂B₂C₂，…按此规律，经过2015次操作后△A₂₀₁₅B₂₀₁₅C₂₀₁₅的面积为_____________．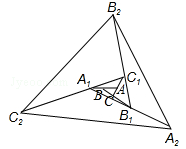

如图，在Rt△ADB中，∠D=90°，C为AD上一点，则可能是（     ）

A．10°

B．20°

C．30°

D．40°

如图，在△ABC中，∠BAC=90°，AB=AC=6，D为BC的中点．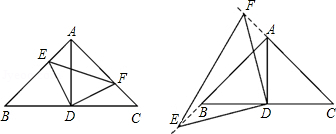

（1）若E、F分别是AB、AC上的点，且AE=CF，求证：△AED≌△CFD；
（2）当点F、E分别从C、A两点同时出发，以每秒1个单位长度的速度沿CA、AB运动，到点A、B时停止；设△DEF的面积为y，F点运动的时间为x，求y与x的函数关系式；
（3）在（2）的条件下，点F、E分别沿CA、AB的延长线继续运动，求此时y与x的函数关系式．

（本题共12分）课本的作业题中有这样一道题：把一张顶角为36°的等腰三角形纸片剪两刀，分成3张小纸片，使每张小纸片都是等腰三角形，你能办到吗？请画示意图说明剪法．
我们有多种剪法，图1是其中的一种方法：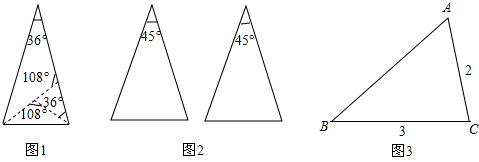

定义：如果两条线段将一个三角形分成3个等腰三角形，我们把这两条线段叫做这个三角形的三分线．
（1）请你在图2中用两种不同的方法画出顶角为45°的等腰三角形的三分线，并标注每个等腰三角形顶角的度数；（若两种方法分得的三角形成3对全等三角形，则视为同一种）
（2）△ABC中，∠B=30°，AD和DE是△ABC的三分线，点D在BC边上，点E在AC边上，且AD=BD，DE=CE，设∠C=x°，试画出示意图，并求出x所有可能的值；
（3）如图3，△ABC中，AC=2，BC=3，∠C=2∠B，请画出△ABC的三分线，并求出三分线的长．

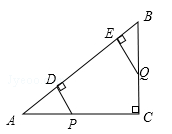
如图，在Rt△ABC中，∠C=90°，AC=8，BC=6，P、Q是边AC、BC上的两个动点， PD⊥AB于点D， QE⊥AB于点E．设点P、Q运动的时间是t秒（t＞0）．若点P从C点出发沿CA以每秒3个单位的速度向点A匀速运动，到达点A后立刻以原来的速度沿AC返回到点C停止运动；点Q从点B出发沿BC以每秒1个单位的速度向点C匀速运动，到达点C后停止运动 ，当t=             时，△APD和△QBE全等．

 

如图，△ABC的面积为1，第一次操作：分别延长AB，BC，CA，至点A₁，B₁，C₁，使A₁B=AB，B₁C=2BC，C₁A=2CA，顺次连接A₁，B₁，C₁，得到△A₁B₁C₁．第二次操作：分别延长A₁B₁，B₁C₁，C₁A₁至点A₂，B₂，C₂，使A₂B₁=A₁B₁，B₂C₁=2B₁C₁，C₂A₁=2C₁A₁，顺次连接A₂，B₂，C₂，得到△A₂B₂C₂，按此规律，要是得到的三角形的面积为38416，需要经过        次操作．

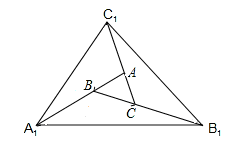
如图，已知△ABC中，∠B="90" º，AB=16cm，BC=12cm，P、Q是△ABC边上的两个动点，其中点P从点A开始沿A→B方向运动，且速度为每秒1cm，点Q从点B开始沿B→C→A方向运动，且速度为每秒2cm，它们同时出发，设出发的时间为t秒．

（1）出发2秒后，求PQ的长；
（2）当点Q在边BC上运动时，出发几秒钟后，△PQB能形成等腰三角形？
（3）当点Q在边CA上运动时，求能使△BCQ成为等腰三角形的运动时间．

（本小题满分8分）如图，平面直角坐标系中，将含30°的三角尺的直角顶点C落在第二象限．其斜边两端点A、B分别落在x轴、y轴上，且AB=12cm

（1）若OB=6cm．
①求点C的坐标；
②若点A向右滑动的距离与点B向上滑动的距离相等，求滑动的距离；
（2）点C与点O的距离的最大值．

小明遇到这样一个问题：已知：在△ABC中，AB，BC，AC三边的长分别为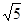、、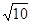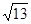，求△ABC的面积．
小明是这样解决问题的：如图1所示，先画一个正方形网格（每个小正方形的边长为1），再在网格中画出格点△ABC（即△ABC三个顶点都在小正方形的顶点处），从而借助网格就能计算出△ABC的面积．他把这种解决问题的方法称为构图法．请回答：

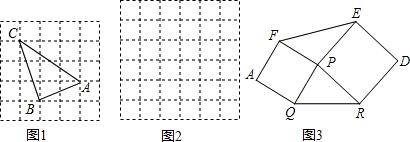
（1）求图1中△ABC的面积；
参考小明解决问题的方法，完成下列问题：
（2）图2是一个6×6的正方形网格（每个小正方形的边长为1）．
①利用构图法在答题卡的图2中画出三边长分别为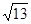、、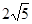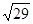的格点△DEF；
②计算△DEF的面积是           ．
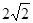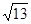（3）如图3，已知△PQR，以PQ，PR为边向外作正方形PQAF，PRDE，连接EF．若PQ=，PR=，QR=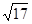，求六边形AQRDEF的面积．

如图△ABC中，AB=10，AC=6，中线AD=4，则BC长是           ．

（本题5分）如图，将一根15cm长的细木棒放入长、宽、高分别为4cm，3cm和12cm的长方体无盖盒子中，则细木棒露在外面的最短长度是多少？

如图，BE、CF分别是△ABC的高，M为BC的中点， EF=5cm，BC=8cm，则△EFM的周长是      cm．

如图，△ABC中，∠C＝90°，∠BAC的平分线交BC于点D，若CD＝3，则点D到AB的距离是      ．