初中数学计算题

先化简，再求值：，其中a是方程的一个根。

如图，抛物线y=x²﹣3x﹣18与x轴交于A、B两点，与y轴交于点C，连接BC、AC．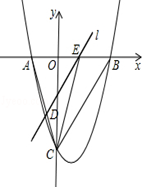

（1）求AB和OC的长；
（2）点E从点A出发，沿x轴向点B运动（点E与点A、B不重合），过点E作直线l平行BC，交AC于点D．设AE的长为m，△ADE的面积为s，求s关于m的函数关系式，并写出自变量m的取值范围；
（3）在（2）的条件下，连接CE，求△CDE面积的最大值；此时，求出以点E为圆心，与BC相切的圆的面积（结果保留π）．

解方程组：
（1）（2）

在△ABC中，P是BC边上的一个动点，以AP为直径的⊙O分别交AB、AC于点E和点F．

（1）若∠BAC＝45°，EF＝4，则AP的长为多少？
（2）在（1）条件下，求阴影部分面积．
（3）试探究：当点P在何处时，EF最短？请直接写出你所发现的结论，不必证明．

计算：

如图，A、B两地相距50千米，甲于某日下午1时骑自行车从A地出发驶往B地，乙也于同日下午骑摩托车从A地出发驶往B地，图中PQR和线段MN，分别表示甲和乙所行驶的S与该日下午时间t之间的关系，试根据图形回答：

⑴甲出发几小时，乙才开始出发
⑵乙行驶多少分钟赶上甲，这时两人离B地还有多少千米？
⑶甲从下午2时到5时的速度是多少？　
⑷乙行驶的速度是多少？

(本题满分8分)
哈尔滨市某校七年级实行小组合作学习，为了解学生课堂发言情况，随机抽取该年级部分学生，对他们每天在课堂上发言的次数进行调查和统计，统计表如下，并绘制了两幅不完整的统计图．已经知A、B两组发言人数直方图高度比为1∶5．

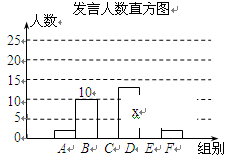
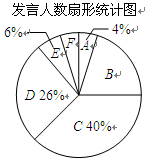
请结合图中相关的数据回答下列问题：
(1)本次调查的样本容量是多少？
(2)求出C组的人数并补全直方图．
(3)该校七年级共有250人，请估计全年级每天在课堂上发言次数不少于15次的人数．

（1）计算：；
（2）已知，化简：．

华联超市文具部的某种毛笔每支售价25元，书法练习本每本售价5元.该商场为促销制定了两种优惠办法：①买一支毛笔就赠送一本书法练习本;②按购买金额打9折付款.某校欲为校书法兴趣小组购买这种毛笔10支，书法练习本x（x≥10）本.
比较购买同样多的书法练习本时，按哪种优惠办法付款更省钱;

(10分)如图：一次函数y=－x+6的图象与x轴和y轴分别交于点A和B ,再将△AOB
沿直线CD对折，使点A与点B重合。直线CD与x轴交于点C,与AB交于点D。

(1)点A的坐标为，点B的坐标为。
(2)求OC的长度 ；
(3)在x轴上有一点P，且△PAB是等腰三角形,不需计算过程，请直接写出点P的坐标 。

(10分) 某通讯公司推出①、②两种手机通话月收费方式供用户选择，其中一种有月租费，另一种无月租费，且两种收费方式的月通话时间x（分钟）与收费y（元）之间的函数关系如图所示．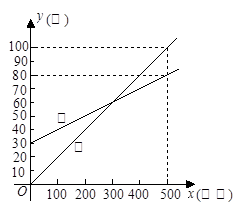

（1）有月租费的收费方式是（填①或②），月租费是元；
（2）分别求出①，②两种收费方式中y与自变量x之间的函数关系式；
（3）请你根据用户月通话时间的多少，给出经济实惠的选择建议

(8分)如图：△ABC中，AD是高，CE是中线，G是CE的中点，DG⊥CE，G为垂足。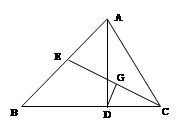

请说明下列结论成立的理由：
（1）DC＝BE； （2）∠B＝2∠BCE 。

如图所示，OA=OD，OB=OC，请说明下列结论成立的理由：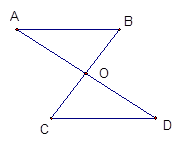

(1）△AOB≌△DOC； (2）AB∥CD

甲、乙两个工程队分别同时开挖两段100m河渠，所挖河渠的长度与挖掘时间之间的关系如图所示，请根据图象所提供的信息解答下列问题：

⑴乙队开挖到30m时，用了　　　　h．开挖6h时甲队比乙队多挖了　　　m；
⑵请你求出：
①甲队在的时段内，与之间的函数关系式；
②乙队在的时段内，与之间的函数关系式；
⑶若两队此后速度不变，几小时后，甲队没有完工的河渠的长度不足乙队没有完工的河渠的长度一半？

某文化用品商店用2000元购进一批学生书包，面市后发现供不应求，商店又购进第二批同样的书包，所购数量是第一批购进数量的3倍，但单价贵了4元，结果第二批用了6300元。
⑴求第一批购进书包的单价是多少元？
⑵若商店销售这两批书包时，每个售价都是120元，全部售出后，商店共盈利多少元？