初中数学计算题

先化简再求值：（，
其中x＝1＋，y＝1－；

计算：^-2＋（π－1）⁰＋tan60°－；　　

计算：（每小题4分，共16分）
⑴⑵
⑶ ．⑷

计算：
（1）（2）
（3）（4）

（本小题满分12分）
如图，在平面直角坐标系中，矩形OABC的两边分别在x轴和y轴上，OA="16" cm， OC=8cm，现有两动点P、Q分别从O、C同时出发，P在线段OA上沿OA方向以每秒2cm的速度匀速运动，Q在线段CO上沿CO方向以每秒1cm的速度匀速运动．设运动时间为t秒．
（1）用含t的式子表示△OPQ的面积S；
（2）判断四边形OPBQ的面积是否是一个定值，如果是，请求出这个定值；如果不是，请说明理由；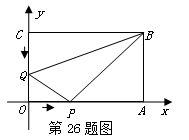
（3）当△OPQ∽△ABP时，抛物线y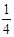＝x²+bx+c经过B、P两点，求抛物线的解析式；
（4）在（3）的条件下，过线段BP上一动点M作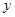轴的平
行线交抛物线于N，求线段MN的最大值．

（本小题满分10分）
某商场试销一种成本为每件60元的服装，经试销发现，销售量（件）与销售单价（元）符合一次函数，且时，；时，．
（1）求一次函数的表达式；
（2）若该商场获得利润为元，试写出利润与销售单价之间的关系式；
（3）若该商场想获得500元的利润且尽可能地扩大销售量，则销售单价应定为多少元？
（4）销售单价定为多少元时，商场可获得最大利润，最大利润是多少元？

（本小题满分8分）“知识改变命运，科技繁荣祖国”．我市中小学每年都要举办一届科技运动会．下图为我市某校2011年参加科技运动会航模比赛（包括空模、海模、车模、建模四个类别）的参赛人数统计图：

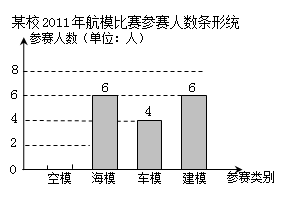（1）该校参加车模、建模比赛的人数分别是人和人；
（2）该校参加航模比赛的总人数是人，空模所在扇形的圆心角的度数是°，
并把条形统计图补充完整；
（3）从全市中小学参加航模比赛选手中随机抽取80人，其中有32人获奖．今年我市中小学参加航模比赛人数共2485人，请你估算今年参加航模比赛的获奖人数约是多少人?

、计算：

一只箱子里原有3个球，其中2个白球，1个红球，它们除颜色外均相同．
（1）从箱子中任意摸出两个球，用树状图或列表法列举出所有可能并求两次摸出球的都是白球的概率．
（2）若从箱子中任意摸出一个球是红球的概率为，则需要再加入几个红球？．

计算：||

计算：

如图，已知△ABC为直角三角形，∠ACB＝90°，AC＝BC，点A、C在x轴上，点B坐标为（3，m）(m＞0)，线段AB与y轴相交于点D，以P（1，0）为顶点的二次函数图像经过点B、D．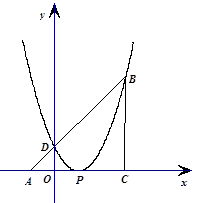

请直接写出用m表示点A、D的坐标
求这个二次函数的解析式；
点Q为二次函数图像上点P至点B之间的一点，连结PQ、BQ，求四边形ABQP面积的最大值．

解方程.

足球比赛的记分规则为：胜一场得3分，平一场得1分，输一场得0分.一支足球队在某个赛季中共需比赛14场,现已比赛了8场,输了1场,得17分. 请问:
(1)前8场比赛中,这支球队共胜了多少场?
(2)这支球队打满14场比赛,最高能得多少分?
(3)通过对比赛情况的分析,这支球队打满14场比赛,得分不低于29分,就可以达到预期的目标.请你分析一下,在后面的6场比赛中,这支球队至少要胜几场,才能达到预期目标?

甲、乙两件服装的成本共500元，商店老板为获取利润，决定将甲服装按50﹪的利润定价，乙服装按40﹪的利润定价。在实际出售时，应顾客要求，两件服装均按9折出售，这样商店共获利157元，求甲、乙两件服装的成本各是多少元？