初中数学填空题

如图，二次函数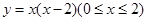的图象，记为C₁，它与x轴交于点O，A₁；将C₁绕点A₁旋转180°得C₂，交x轴于点A₂；将C₂绕点A₂旋转180°得C₃，交x轴于点A₃；……如此进行下去，直至得C₁₄. 若P(27,m)在第14段图象C₁₄上，则m＝．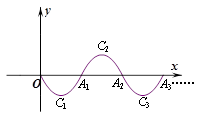

矩形A₁B₁C₁O，A₂B₂C₂C₁，A₃B₃C₃C₂，…按如图所示放置．点A₁，A₂，A₃，A₄…和点C₁，C₂，C₃，C₄…，分别在直线(k＞0)和x轴上，若点B₁(1，2)，B₂(3，4)，且满足,则直线的解析式为，点的坐标为，点的坐标为_．

如右图，正六边形ABCDEF的边长为2，两顶点A、B分别在x轴和y轴上运动，则顶点D到原点O的距离的最大值和最小值的乘积为．

如图，直角三角形ABO放置在平面直角坐标系中，已知斜边OA在x轴正半轴上，且OA＝4，AB＝2，将该三角形绕着点O逆时针旋转120°后点B的对应点恰好落在一反比例函数图像上，则该反比例函数的解析式为．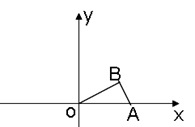

如图所示中的∠A的正切值为．

如图，已知∠AOB=α，在射线OA、OB上分别取点OA₁=OB₁，连接A₁B₁，在B₁A₁、B₁B上分别取点A₂、B₂，使B₁B₂=B₁A₂，连接A₂B₂…按此规律下去，记∠A₂B₁B₂=θ₁，∠A₃B₂B₃=θ₂，…，∠A_n+1B_nB_n+1=θ_n，
则（1）θ₁=, （2）θ_n=.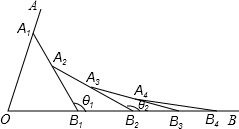

把数字按如图所示排列起来，从上开始，依次为第一行、第二行、第三行……，中间用虚线围的一列，从上至下依次为1、5、13、25、…，则第10个数为．

如图，在Rt△ABC中，∠ABC = 90, AB =" 8cm" , BC =" 6cm" , 分别以A,C为圆心，以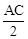的长为半径作圆, 将 Rt△ABC截去两个扇形，则剩余（阴影）部分的面积为cm（结果保留π）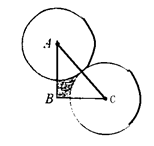

如图，在正方形ABCD中，边长为2的等边三角形AEF的顶点E、F分别在BC和CD上，下列结论：
①CE=CF；②∠AEB=75°；③BE+DF=EF；④S_{正方形ABCD}=2+
其中正确的序号是______________

如图，直线l:，点A₁坐标为(0，1)，过点A₁作y轴的垂线交直线l于点B₁，以原点O 为圆心，OB₁长为半径画弧交y一轴于点A₂；再过点A₂作y轴的垂线交直线于点B₂，以原点O为圆心，OB₂长为半径画弧交y轴于点A₃，…，按此做法进行下去，点A₄的坐标为(_______，_______)；点A_n的坐标为(_______，_______)．

如图，□ABCD中，AC⊥AB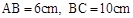．，E是CD上的点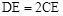，．点P从D点出发，以1cm/s的速度沿DA运动至A点停止．则当△EDP为等腰三角形时，点P的运动时间为　　　．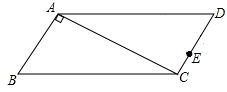

如图，在反比例函数（x > 0）的图象上有点A₁，A₂，A₃，…，A_n-1，A_n，这些点的横坐标分别是1，2，3，…，n -1，n时，点A₂的坐标是__________；过点A₁作x轴的垂线，垂足为B₁，再过点A₂作A₂ P₁⊥A₁ B₁于点P₁，以点P₁、A₁、A₂为顶点的△P₁A₁A₂的面积记为S₁，按照以上方法继续作图，可以得到△P₂ A₂A₃，…，△P _n-1 A_n-1 A_n，其面积分别记为S₂，…，S_n-1，则S₁+ S₂+…+ S_n=________．

如图，已知直线y=x+4与两坐标轴分别交于A、B两点，⊙C的圆心坐标为 （2，O），半径为2，若D是⊙C上的一个动点，线段DA与y轴交于点E，则△ABE面积的最小值和最大值分别是　　．

已知菱形ABCD的两条对角线的长分别为6和8，M、N分别是边BC、CD的中点，P是对角线BD上一点，则PM+PN的最小值=　　．

如图，在函数（x＞0）的图象上有点P₁、P₂、P₃…、P_n、P_n+1，点P₁的横坐标为2，且后面每个点的横坐标与它前面相邻点的横坐标的差都是2，过点P₁、P₂、P₃…、P_n、P_n+1分别作x轴、y轴的垂线段，构成若干个矩形，如图所示，将图中阴影部分的面积从左至右依次记为S₁、S₂、S₃…、S_n，则S₁=　_______　，S_n=　_________　．（用含n的代数式表示）